Tìm số đo các góc của tam giác ABC, biết rằng các số đo này tỉ lệ với 2, 3 và 4
Mặc dù nhìn giống hình như đó là đại đấy
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\dfrac{\widehat{A}}{3}=\dfrac{\widehat{B}}{5}=\dfrac{\widehat{C}}{7}=\dfrac{\widehat{A}+\widehat{B}+\widehat{C}}{3+5+7}=\dfrac{180^0}{15}=12^0\\ \Rightarrow\left\{{}\begin{matrix}\widehat{A}=36^0\\\widehat{B}=60^0\\\widehat{C}=84^0\end{matrix}\right.\)

cả 2 phần cậu đều áp dụng tính chất dãy tỉ số bằng nhau đi
dễ mà

1>chiều dài là:
12:(5-2)x5=20
chiều rộng là:
20-12=8
2> chiều rộng là:
60:5x2=24
chiều dài là:
60-24=36
2> góc 1 là: 180:9x2=40
góc 2 là: 180:9x3=60
góc 3 là: 180-60-40=80
**** cho minh nha
1.
Đáp án:
Chu vi hình chữ nhật là 56m56m
Giải thích các bước giải:
Gọi chiều dài và chiều rộng của hình CN là a;b (m); (a;b > 0)
Theo bài ra ta có :
b2b2 == a5a5 và aa −− bb == 1212
Áp dụng t/c dãy tỉ số = nhau ta có :
a2a2 == b5b5 == a−b5−2a−b5−2 == 123123 == 44
⇒⇒ a2a2 == 44 ⇒⇒ aa == 22 .. 44 == 88 m
và b5b5 == 44 ⇒⇒ bb == 55 .. 44 == 2020 m
Chu vi hình CN là :
(( 88 ++ 2020 )) .. 22 == 5656 (m)
Vậy chu vi hình chữ nhật là 5656 m
2.
Nửa chu vi là:
60 :2=30 (m)60 :2=30 (m)
Theo bài ra:
ab=23ab=23
⇒a=23b⇒a=23b
Ta có:
a+b=30a+b=30
⇒23b+b=30⇒23b+b=30
⇒23b+33b=30⇒23b+33b=30
⇒53b=30⇒53b=30
⇒b=30:53⇒b=30:53
⇒b=18⇒b=18
Nên chiều dài là 18 m18 m và chiều rộng là 30−18=12 m
3.
Gọi số đo ba góc của tam giác ABC lần lượt là A,B,C
Theo đề bài ,ta có:
A/1=B/2=C/3 và A+B+C=180
=>A/1=B/2=C/3=(A+B+C)/(1+2+3)=(A+B+C)/6=180/6=30
Do đó:
+)A/1=30=>A=30
+)B/2=30=>B=60
+)C/3=30=>C=90
Vậy số đo ba góc của tam giác ABC lần lượt là :30,60,90
Vậy tam giác ABC là tam giác vuông
HT

Gọi a, b, c (độ) lần lượt là số đo 3 góc A, B, C. (0 < a; b; c < 180º).
Theo định lí tổng ba góc của tam giác ta có:
a + b + c = 180.
Vì số đo 3 góc tỉ lệ với 3; 5; 7 nên ta có:
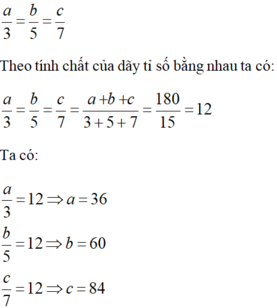
Vậy số đo ba góc của tam giác ABC là: 36o; 60o; 84o
Số đo các góc của tam giác ABC là \(\widehat{A},\widehat{B,}\widehat{C}.\) Giả sử theo thứ tự đó, các góc này tỉ lệ với 2, 3 và 4, nghĩa là \(\widehat{A}\div\widehat{B}\div\widehat{C}=2\div3\div4\) hay \(\frac{\widehat{A}}{2}=\frac{\widehat{B}}{3}=\frac{\widehat{C}}{4}=\frac{\widehat{A}+\widehat{B}+\widehat{C}}{2+3+4}=\frac{180^o}{9}\)
Từ đó suy ra: \(\widehat{A}=40^o,\widehat{B}=60^o,\widehat{C}=80^o\)
Gọi a,b,c lần lượt là độ dài cạnh I, cạnh II, cạnh III của tam giác (a,b,c ϵ N* ; a,b,c < 180)
Ta có:
\(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}\) và \(\left(a+b+c=180^o\right)\)
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}=\frac{a+b+c}{2+3+4}=\frac{180^o}{9}=20^o\)
Suy ra
Độ dài cạnh I là: 20o . 2 = 40o
Độ dài cạnh II là: 20o . 3 = 60o
Độ dài cạnh III là: 20o . 4 = 80o