Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\dfrac{\widehat{A}}{3}=\dfrac{\widehat{B}}{5}=\dfrac{\widehat{C}}{7}=\dfrac{\widehat{A}+\widehat{B}+\widehat{C}}{3+5+7}=\dfrac{180^0}{15}=12^0\\ \Rightarrow\left\{{}\begin{matrix}\widehat{A}=36^0\\\widehat{B}=60^0\\\widehat{C}=84^0\end{matrix}\right.\)

cả 2 phần cậu đều áp dụng tính chất dãy tỉ số bằng nhau đi
dễ mà

1>chiều dài là:
12:(5-2)x5=20
chiều rộng là:
20-12=8
2> chiều rộng là:
60:5x2=24
chiều dài là:
60-24=36
2> góc 1 là: 180:9x2=40
góc 2 là: 180:9x3=60
góc 3 là: 180-60-40=80
**** cho minh nha
1.
Đáp án:
Chu vi hình chữ nhật là 56m56m
Giải thích các bước giải:
Gọi chiều dài và chiều rộng của hình CN là a;b (m); (a;b > 0)
Theo bài ra ta có :
b2b2 == a5a5 và aa −− bb == 1212
Áp dụng t/c dãy tỉ số = nhau ta có :
a2a2 == b5b5 == a−b5−2a−b5−2 == 123123 == 44
⇒⇒ a2a2 == 44 ⇒⇒ aa == 22 .. 44 == 88 m
và b5b5 == 44 ⇒⇒ bb == 55 .. 44 == 2020 m
Chu vi hình CN là :
(( 88 ++ 2020 )) .. 22 == 5656 (m)
Vậy chu vi hình chữ nhật là 5656 m
2.
Nửa chu vi là:
60 :2=30 (m)60 :2=30 (m)
Theo bài ra:
ab=23ab=23
⇒a=23b⇒a=23b
Ta có:
a+b=30a+b=30
⇒23b+b=30⇒23b+b=30
⇒23b+33b=30⇒23b+33b=30
⇒53b=30⇒53b=30
⇒b=30:53⇒b=30:53
⇒b=18⇒b=18
Nên chiều dài là 18 m18 m và chiều rộng là 30−18=12 m
3.
Gọi số đo ba góc của tam giác ABC lần lượt là A,B,C
Theo đề bài ,ta có:
A/1=B/2=C/3 và A+B+C=180
=>A/1=B/2=C/3=(A+B+C)/(1+2+3)=(A+B+C)/6=180/6=30
Do đó:
+)A/1=30=>A=30
+)B/2=30=>B=60
+)C/3=30=>C=90
Vậy số đo ba góc của tam giác ABC lần lượt là :30,60,90
Vậy tam giác ABC là tam giác vuông
HT

Gọi a, b, c (độ) lần lượt là số đo 3 góc A, B, C. (0 < a; b; c < 180º).
Theo định lí tổng ba góc của tam giác ta có:
a + b + c = 180.
Vì số đo 3 góc tỉ lệ với 3; 5; 7 nên ta có:
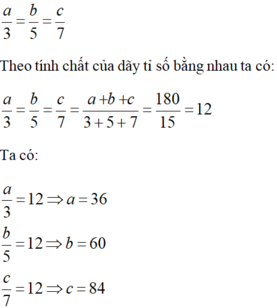
Vậy số đo ba góc của tam giác ABC là: 36o; 60o; 84o

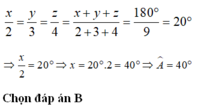
Số đo các góc của tam giác ABC là \(\widehat{A},\widehat{B,}\widehat{C}.\) Giả sử theo thứ tự đó, các góc này tỉ lệ với 2, 3 và 4, nghĩa là \(\widehat{A}\div\widehat{B}\div\widehat{C}=2\div3\div4\) hay \(\frac{\widehat{A}}{2}=\frac{\widehat{B}}{3}=\frac{\widehat{C}}{4}=\frac{\widehat{A}+\widehat{B}+\widehat{C}}{2+3+4}=\frac{180^o}{9}\)
Từ đó suy ra: \(\widehat{A}=40^o,\widehat{B}=60^o,\widehat{C}=80^o\)
Gọi a,b,c lần lượt là độ dài cạnh I, cạnh II, cạnh III của tam giác (a,b,c ϵ N* ; a,b,c < 180)
Ta có:
\(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}\) và \(\left(a+b+c=180^o\right)\)
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}=\frac{a+b+c}{2+3+4}=\frac{180^o}{9}=20^o\)
Suy ra
Độ dài cạnh I là: 20o . 2 = 40o
Độ dài cạnh II là: 20o . 3 = 60o
Độ dài cạnh III là: 20o . 4 = 80o