cho hình chữ nhật ABCD AD<AB<2AD vẽ tam giác ABI, CDK vào trong hình chữ nhật I=K=90 E,K lần lượt là giao điểm của AI,DK và CK,CI .a chứng minh EF//CD b tứ giác EKFI là hình vuôngcho hình chữ nhật ABCD AD<AB<2AD vẽ tam giác ABI, CDK vào trong hình chữ nhật I=K=90 E,K lần lượt là giao điểm của AI,DK và CK,CI .a chứng minh EF//CD b tứ giác EKFI là hình vuông
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
18 tháng 7 2017
Đọ dài cạnh AD là: 2 x 2 = 4 (cm)
Diện tích hình chữ nhật ABCD là: 4 × 2 = 8 ( c m 3 )
15 tháng 12 2021
diện tích hình chữ nhật là : 12*24=288(cm2)
chiều cao bằng chiều rộng
chiều dài bằng đáy hình tam giác
Diện tích hình tam giác là: 288:2=144(cm2)
Đáp số : 144 cm2
CM
4 tháng 9 2018
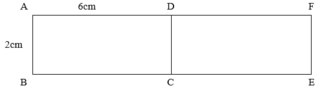
AF = 2 AD => AF = 2 × 6 = 12cm và DF = AD = 6cm
BE = 2 BC => BE = 2 × 6 = 12cm và CE = BC = 6cm
Suy ra EFDC là hình chữ nhật do có CD = EF và DF = CE và góc FDC và góc DCE là góc vuông
Diện tích hình chữ nhật ABCD bằng:
AB × AD = 2 × 6 = 12 (cm2)
Diện tích hình chữ nhật DCEF là:
DC × DF = 2 × 6 = 12 (cm2)
Diện tích hình chữ nhật ABEF là :
AB × AF = 2 × 12 = 24 (cm2)
Đáp số: SABCD = SDCEF = 12 cm2; SABEF = 24cm2
N
2
BF
11 tháng 3 2023
Áp dụng định lý Pitago vào `ΔABD`
`=> AD^2 + AB^2 = BC^2`
`=> AD^2 = BC^2 - AB^2 `
`=> AD^2 = 13^2 - 12^2 `
`=> AD^2 = 25`
`=> AD = 5 (`Vì `AD > 0)`
`S_(ABCD) = 5 xx 12 = 60`
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 3 2023
Áp dụng định lý Pitago trong tam giác vuông ABD:
\(AD=\sqrt{BD^2-AB^2}=\sqrt{13^2-12^2}=5\)
\(S_{ABCD}=AB.AD=60\)
5 tháng 7 2023
Hạ đường cao AH của tam giác ABD => AH=14,4cm
Pytago => AD^2-AH^2=DH^2
=> DH^2=116,64
=> DH=10,8cm
HT lượng => HA^2=HB.HC
=> HB=HA^2/HB=14,4^2/10,8=19,2cm
=> BD=HD+HB=10,8+19,2=30m
Pytago => AB^2=AH^2+HB^2=576
=> AB=24cm
=> chu vi HCN ABCD là: 2(AB+AD)=2(18+24)=84(cm^2)