Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì E thuộc cạnh AB nên EB < AB hay 2x < y
Ta có: AE = AB – EB = y – 2x (cm)
AG = AD + DG = y + (3/2) EB = y + (3/2) .2x = y + 3x (cm)
Diện tích hình chữ nhật bằng diện tích hình vuông nên ta có phương trình:
(y – 2x)(y + 3x) = y 2
Theo định lí Pitago, ta có: F C 2 = E B 2 + D G 2
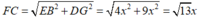
Chu vi ngũ giác ABCFG:
PABCFG = AB + BC + CF + FG + GA
= AB + BC + CF + FG + GD + DA
= y + y + x 13 + y – 2x + 3x + y = x(1 + 13 ) + 4y
Vì chu vi ngũ giác ABCFG bằng 100 + 4 13 (cm) nên ta có phương trình:
x(1 + 13 ) + 4y = 100 + 4 13
Ta có hệ phương trình:
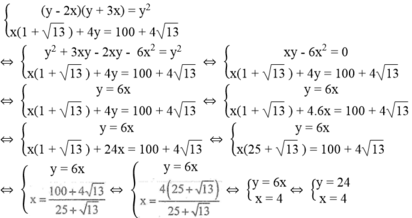
Giá trị của x và y thỏa điều kiện bài toán.
Vậy x = 4 (cm), y = 24 (cm).

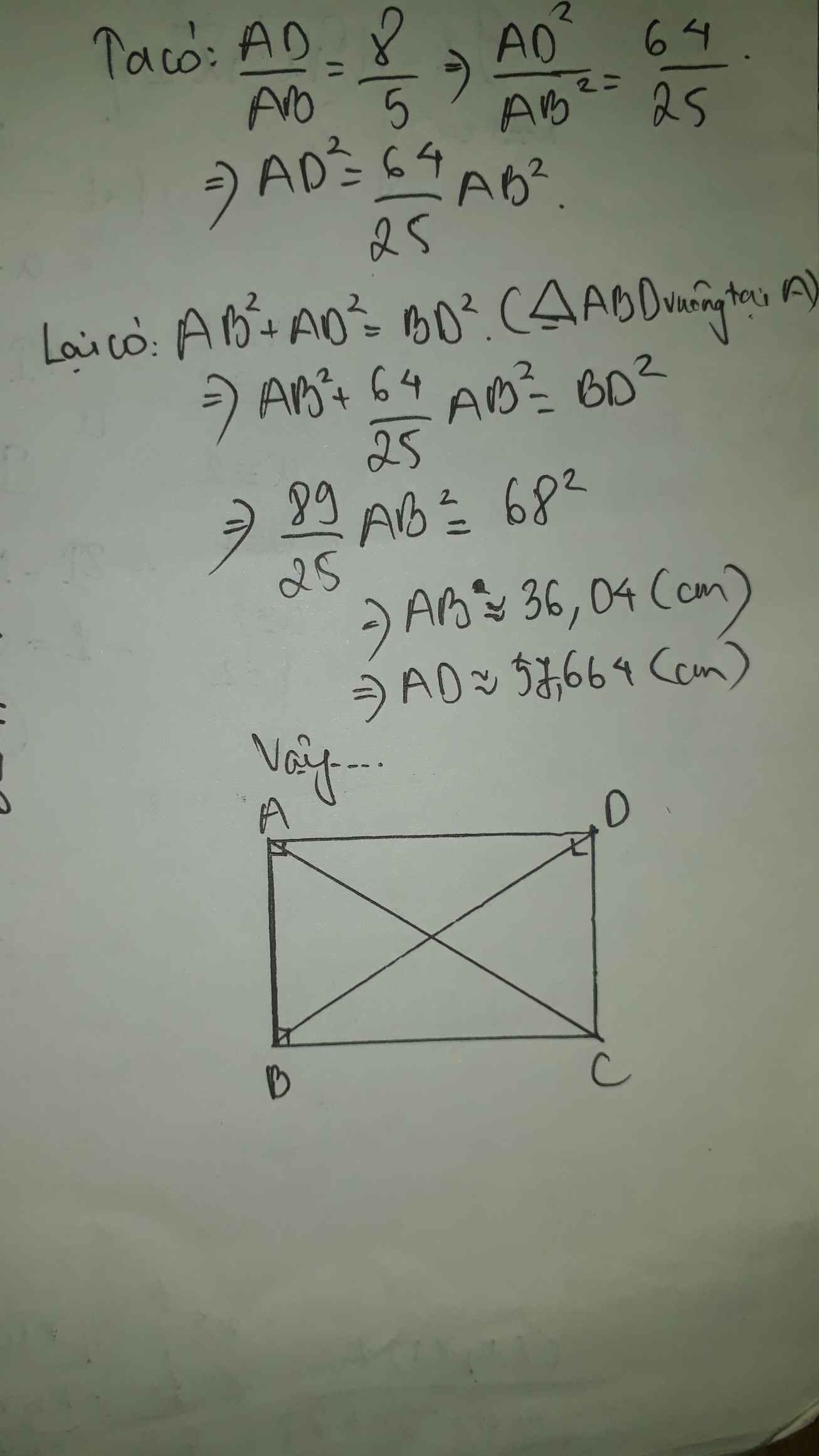
Ta có: \(\dfrac{AD}{AB}=\dfrac{8}{15}\)
nên \(AD=\dfrac{8}{15}AB\)
Áp dụng định lí Pytago vào ΔABD vuông tại A, ta được:
\(BD^2=AD^2+AB^2\)
\(\Leftrightarrow\left(\dfrac{8}{15}AB\right)^2+AB^2=68^2=4624\)
\(\Leftrightarrow AB^2\cdot\dfrac{289}{225}=4624\)
\(\Leftrightarrow AB^2=3600\)
\(\Leftrightarrow AB=60\left(cm\right)\)
\(\Leftrightarrow AD=\dfrac{8}{15}AB=\dfrac{8}{15}\cdot60=32\left(cm\right)\)
\(\Leftrightarrow CD=60cm;BC=32cm\)

ΔADC vuông tại D
=>\(AC^2=AD^2+DC^2\)
=>\(AC^2=8^2+6^2=100\)
=>AC=10(cm)
ABCD là hình chữ nhật
=>AC cắt BD tại trung điểm của mỗi đường và AC=BD
=>M là trung điểm chung của AC và BD và AC=BD
=>MD=MB=MA=MC=AC/2=5(cm)
Xét ΔDME vuông tại M và ΔDCB vuông tại C có
\(\widehat{MDE}\) chung
Do đó: ΔDME đồng dạng với ΔDCB
=>\(\dfrac{ME}{CB}=\dfrac{DM}{DC}\)
=>\(\dfrac{ME}{6}=\dfrac{5}{8}\)
=>\(ME=3,75\left(cm\right)\)

Áp dụng định lý Pitago cho tam giác vuông ABC
\(AC=\sqrt{AB^2+BC^2}=10\left(cm\right)\)
Áp dụng hệ thức lượng cho tam giác vuông ABC với đường cao BE:
\(AB^2=AE.AC\Rightarrow AE=\dfrac{AB^2}{AC}=6,4\left(cm\right)\)
\(AB.AC=BE.AC\Rightarrow AE=\dfrac{AB.AC}{BC}=4,8\left(cm\right)\)
b.
Ta có: \(EC=AC-AE=3,6\left(cm\right)\)
Do AB song song CF, theo định lý Talet:
\(\dfrac{CF}{AB}=\dfrac{CE}{AE}\Rightarrow CF=\dfrac{AB.CE}{AE}=4,5\left(cm\right)\)
\(\Rightarrow DF=DC-CF=8-4,5=3,5\left(cm\right)\)
Áp dụng định lý Pitago cho tam giác vuông ADF:
\(AF=\sqrt{AD^2+DF^2}=\dfrac{\sqrt{193}}{2}\left(cm\right)\)
Pitago tam giác vuông BCF:
\(BF=\sqrt{BC^2+CF^2}=7,5\left(cm\right)\)
Kẻ FH vuông góc AB \(\Rightarrow ADFH\) là hình chữ nhật (tứ giác 3 góc vuông)
\(\Rightarrow FH=AD=6\left(cm\right)\)
\(S_{ABF}=\dfrac{1}{2}FH.AB=\dfrac{1}{2}.6.8=24\left(cm^2\right)\)
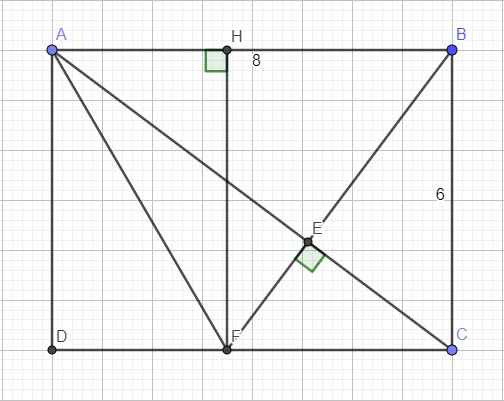
A B C D
Áp dụng định lý Pitago vào `ΔABD`
`=> AD^2 + AB^2 = BC^2`
`=> AD^2 = BC^2 - AB^2 `
`=> AD^2 = 13^2 - 12^2 `
`=> AD^2 = 25`
`=> AD = 5 (`Vì `AD > 0)`
`S_(ABCD) = 5 xx 12 = 60`
Áp dụng định lý Pitago trong tam giác vuông ABD:
\(AD=\sqrt{BD^2-AB^2}=\sqrt{13^2-12^2}=5\)
\(S_{ABCD}=AB.AD=60\)