- Số trục đối xứng của hình vuông là
- Nghiệm thuộc khoảng(0;90) của phương trình \(4\sin x-1\) là ? độ (Tính chính xác đến hàng phần trăm).
- Biết B(8; 3) là ảnh của điểm A(7; -2) qua phép tịnh tiến theo véctơ v . Khi đó tọa độ của véctơv bằng (.........). (nhập hoành độ trước, tung độ sau, ngăn cách nhau bởi dấu ";").
Biết nghiệm thuộc khoảng(\(\frac{\pi}{2};\frac{3\pi}{2}\) )của phương trình\(\sin x-cosx=\sqrt{2}sin2x\) là\(k\pi\) . Khi đó \(6k=......\). (nhập kết quả dưới dạng số thập phân thu gọn)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

* Hình vuông có 4 trục đối xứng gồm 2 đường chéo của hình vuông và 2 đường thẳng đi qua trung điểm từng của cặp cạnh đối diện của hình vuông
* Hinh tròn có vô số trục đối xứng là các đường thẳng đi qua tâm của hình vuông.

Đáp án A
Nhữngphát biểu sai: d; f; i
d) Qua phép đối xứng trục, đoạn thẳng AB biến thành đoạn thẳng song song và bằng nó hoặc là chính nó.
f) Qua phép đối xứng trục Đa, tam giác có một đỉnh nằm trên a sẽ biến thành chính nó ( chỉ trong trường hợp tam giác đều hoặc tam giác cân cóđỉnh nằm trên trục đối xứng)
i) Hình chữ nhật có 2 trục đối xứng

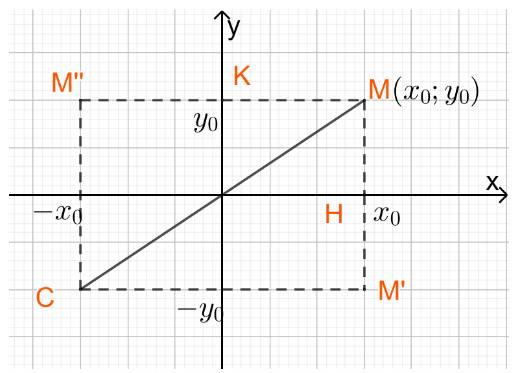
a) H là hình chiếu vuông góc của M trên trục Ox nên tọa độ điểm H là \(H\left( {{x_0};0} \right)\)
b) M’ đối xứng với M qua trục Ox nên H là trung điểm của MM’
Suy ra \({x_{M'}} = 2{x_H} - {x_M} = 2{x_0} - {x_0} = {x_0};{y_{M'}} = 2{y_H} - {y_M} = 2.0 - {y_0} = - {y_0}\)
Vậy tọa độ điểm M’ là \(\left( {{x_0}; - {y_0}} \right)\)
c) K là hình chiếu vuông góc của M trên trục Oy nên tọa độ điểm K là \(K\left( {0;{y_0}} \right)\)
d) M’’ đối xứng với M qua trục Oy nên K là trung điểm của MM’’
Suy ra \({x_{M''}} = 2{x_K} - {x_M} = 2.0 - {x_0} = - {x_0};{y_{M''}} = 2{y_K} - {y_M} = 2{y_0} - {y_0} = {y_0}\)
Vậy tọa độ điểm M'' là \(\left( { - {x_0};{y_0}} \right)\)
e) C đối xứng với M qua gốc tọa độ nên O là trung điểm của MC
Suy ra \({x_C} = 2{x_O} - {x_M} = 2.0 - {x_0} = - {x_0};{y_C} = 2{y_O} - {y_M} = 2.0 - {y_0} = - {y_0}\)
Vậy tọa độ điểm C là \(\left( { - {x_0}; - {y_0}} \right)\)

Các phát biểu về đối xứng hình học như sau:
A. Hình tròn: Hình tròn có vô số trục đối xứng và 1 tâm đối xứng. Điều này đúng.
B. Hình vuông: Hình vuông có 4 trục đối xứng, tương ứng với 4 đường đối xứng qua các đỉnh của hình vuông. Điều này cũng đúng.
C. Hình tam giác đều: Hình tam giác đều có 3 trục đối xứng và 1 tâm đối xứng. Điều này cũng đúng.
D. Hình lục giác đều: Hình lục giác đều có 1 tâm đối xứng và 6 trục đối xứng, tương ứng với 6 đường đối xứng qua các đỉnh của hình lục giác đều. Điều này cũng đúng.
Vậy tất cả các phát biểu đều đúng. 😊

Đáp án B
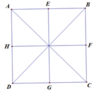
Hình vuông ABCD như hình bên có các trục đối xứng lần lượt là: AC, BD, EG, HF
Tổng cộng có 4 trục đối xứng

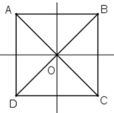
+ Hình vuông cũng là hình bình hành nên nhận O là giao điểm của hai đường chéo là tâm đối xứng.
+ Hình vuông cũng là hình thoi nên nhận hai đường chéo AC và BD là các trục đối xứng.
+ Hình vuông cũng là hình thang cân nên nhận đường thẳng nối trung điểm các cặp cạnh đối diện là trục đối xứng.
Vậy hình vuông có 1 tâm đối xứng và 4 trục đối xứng như trên.



