Chứng minh a=(41+42+43+44+.......+459+460)⋮ 5,⋮ 21
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
21 tháng 11 2019
D = 1 + 4 + 4 2 + 4 3 + . . . + 4 58 + 4 59
= 1 + 4 + 4 2 + 4 3 + 4 4 + 4 5 + ... + 4 57 + 4 58 + 4 59
= 1 + 4 + 4 2 + 4 3 . 1 + 4 + 4 2 + ... + 4 57 . 1 + 4 + 4 2
= 21 + 21 . 4 3 + . . . + 21 . 4 57 ⋮ 21
PT
1
T
19 tháng 9 2023
\(C=1+3+3^2+3^3+\cdot\cdot\cdot+3^{11}\)
\(C=\left(1+3+3^2+3^3\right)+\left(3^4+3^5+3^6+3^7\right)+\left(3^8+3^9+3^{10}+3^{11}\right)\)
\(=\left(1+3+3^2+3^3\right)+3^4\left(1+3+3^2+3^3\right)+3^8\left(1+3+3^2+3^3\right)\)
\(=40+3^4\cdot40+3^8\cdot40\)
\(=40\cdot\left(1+3^4+3^8\right)\)
Vì \(40\cdot\left(1+3^4+3^8\right)⋮40\)
nên \(C⋮40\)
#\(Toru\)
19 tháng 9 2023
\(C=1+3+3^2+3^3+...+3^{11}\)
\(\Rightarrow C=\left(1+3+3^2+3^3\right)+3^4\left(1+3+3^2+3^3\right)+3^8\left(1+3+3^2+3^3\right)\)
\(\Rightarrow C=40+3^4.40+3^8.40\)
\(\Rightarrow C=40\left(1+3^4+3^8\right)⋮40\)
\(\Rightarrow dpcm\)
PT
3
CM
8 tháng 4 2017
A = 1 + 4 + 42 +43 +… + 458 +459
A = (l + 4 + 42) + (43 +44 + 45) + ... + (457+ 458 +459)
A = (1 + 4 + 42) + 43.(1 + 4 + 42) +... + 457 (1 + 4 + 42)
A= 21 + 43.21 + ... + 457.21 .
Do đó A ⋮ 21
14 tháng 7 2017
41 + 42 + 43 + 44 - 21 - 22 - 23 - 24
= (41 - 21) + (42 - 22) + (43 - 23) + (44 - 24)
= 20 + 20 + 20 + 20
= 20 x 4
= 80
tk nha. chúc bn học giỏi :)
NM
1
17 tháng 12 2023
CM: A ⋮ 5
A = 1 + 4 + 42 + 43 + ... + 460
A = (1 + 4) + (42 + 43) + ... + (459 + 460)
A = 5 + 42 . (1 + 4) + ... + 459 . (1 + 4)
A = 5 + 42 . 5 + ... + 459 . 5
A = 5 . (1 + 42 + ... + 459) ⋮ 5
Vậy A ⋮ 5
CM: A ⋮ 21
A = 1 + 4 + 42 + 43 + ... + 460
A = (1 + 4 + 42) + (43 + 44 + 45) + ... + (458 + 459 + 460)
A = 21 + 43 . (1 + 4 + 42) + ... + 458 . (1 + 4 + 42)
A = 21 + 43 . 21 + ... + 458 . 21
A = 21 . (1 + 43 + ... + 458) ⋮ 21
Vậy A ⋮ 21
20 tháng 7 2018
Ta có: \(\frac{1}{41}+\frac{1}{42}+\frac{1}{43}+...+\frac{1}{60}< \frac{1}{40}+\frac{1}{40}+...+\frac{1}{40}=\frac{1}{40}.20=\frac{1}{2}\)
\(\frac{1}{61}+\frac{1}{62}+\frac{1}{63}+...+\frac{1}{80}< \frac{1}{60}+\frac{1}{60}+\frac{1}{60}+...+\frac{1}{60}=\frac{1}{60}.20=\frac{1}{3}\)
\(\Rightarrow\frac{1}{41}+\frac{1}{42}+...+\frac{1}{80}< \frac{1}{2}+\frac{1}{3}=\frac{3}{6}+\frac{2}{6}=\frac{3+2}{6}=\frac{5}{6}\) (đpcm)
Y
6
3 tháng 1 2018
41+42+43+44-21-22-23-24
=( 41- 21 )+ (42-22)+(43-23)+(44-24)
=20 + 20 +20 +20
=20 . 4
=80
DT
Dang Tung
CTVHS
19 tháng 10 2023
B = (4^1 + 4^2) + (4^3 +4^4) + ... + (4^299 + 4^300)
= 4(1+4)+4^3(1+4)+...+4^299(1+4)
= 4.5+4^3 .5 +...+4^299. 5
= 5.(4+4^3+...+4^299) chia hết cho 5
T
19 tháng 10 2023
\(B=4^1+4^2+4^3+4^3+...+4^{300}\\=(4+4^2)+(4^3+4^4)+(4^5+4^6)+...+(4^{299}+4^{300})\\=4\cdot(1+4)+4^3\cdot(1+4)+4^5\cdot(1+4)+...+4^{299}\cdot(1+4)\\=4\cdot5+4^3\cdot5+4^5\cdot5+...+4^{299}\cdot5\\=5\cdot(4+4^3+4^5+...+4^{299})\)
Vì \(5\cdot(4+4^3+4^5+...+4^{299}) \vdots 5\)
nên \(B \vdots 5\)
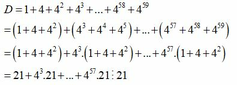
\(A=\left(4^1+4^2+4^3+4^4+...+4^{59}+4^{60}\right)\)
\(=4\left(1+4\right)+...+4^{59}\left(1+4\right)\)
\(=5\left(4+...+4^{59}\right)⋮5\)
\(A=4^1+4^2+4^3+4^4+..+4^{59}+4^{60}\)
\(=4\left(1+4+4^2\right)+...+4^{58}\left(1+4+4^2\right)\)
\(\Leftrightarrow21\left(4+...+4^{58}\right)⋮21\)
=>đpcm