cho đường tròn O, đường kính AB cố định. đường kính CD thay đổi. AC<AD cắt tiếp tuyến tại B lần lượt tại E, F. Tiếp tuyến tại C,D cắt EF tại I, K. M là tđ OB. cm IK vuông góc AK
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án B
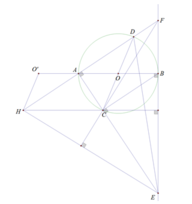
Gọi H là trực tâm tam giác CEF
Ta lại có: C A F ^ = 90 o
3 điểm F, A, H thẳng hàng ⇒ E A H ^ = 90 o
Mà B C E ^ = 90 o
=> A H / / B C A B / / H C
AB = HC = 2R
Gọi O’ làảnh của O qua phép tịnh tiến theo vectơ B A →
OO’ = HC ( = 2R)
MàOO’ // HC ( cùng vuông vớiEF)
O’H = OC = R
Tập hợp H là đường tròn tâm (O’;R)
(CMTT với K là trực tâm tam giác DEF)

a) Ta có: Đường tròn (O;R) có đường kính CD và điểm A nằm trên cung CD => ^CAD=900
=> ^PAQ=900 => \(\Delta\)APQ vuông tại A
Do PQ là tiếp tuyến của (O) tại B => AB là đường cao của \(\Delta\)APQ
=> ^PAB=^AQP (Cùng phụ ^APQ) hay ^CAO=^DQP
Mà \(\Delta\)AOC cân tại O => ^CAO=^ACO => ^DQP=^ACO
Lại có: ^ACO+^PCD=1800 => ^DQP+^PCD=1800
=> Tứ giác CPQD nội tiếp đường tròn (đpcm).
b) Xét \(\Delta\)APQ vuông tại A: Có đường trung tuyến AI => \(\Delta\)AIQ cân tại I
=> ^IAQ=^IQA hay ^IAQ=^DQP => ^IAQ=^ACO (Do ^DQP=^ACO)
Hay ^IAQ=^ACD. Mà ^IAQ+^CAI=900 => ^ACD+^CAI=900
=> AI vuông góc với CD (đpcm).
c) Ta thấy tứ giác CPQD nội tiếp đường tròn
=> 4 đường trung trực của CP;CD;DQ;PQ cắt nhau tại 1 điểm (1)
E là tâm đường tròn ngoại tiếp \(\Delta\)CPQ => Trung trực của CP và CD cắt nhau tại E (2)
Từ (1) và (2) => Điểm E nằm trên trung trực của PQ.
Lại có: I là trung điểm PQ => E là điểm cách PQ 1 khoảng bằng đoạn EI (*)
AB vuông góc PQ; EI cũng vuông góc PQ => AB//EI hay AO//EI (3)
E thuộc trung trực CD; O là trung điểm CD => OE vuông góc CD.
Mà AI vuông góc CD => OE//AI (4)ư
Từ (3) và (4) => Tứ giác AOEI là hình bình hành => AO=EI (**)
Từ (*) và (**) => E là điểm cách PQ 1 khoảng bằng đoạn AO
Mà AO là bk của (O); PQ là tiếp tuyến của (O) tại B
Nên ta có thể nói: Điểm E là điểm cách tiếp tuyến của (O) tại B một khoảng bằng độ dài bán kính của (O)
Vậy khi đường kính CD thay đổi thì điểm E di động trên đường thẳng song song với tiếp tuyến tại B của đường tròn (O) và cách (O) 1 khoảng bằng độ dài bk của (O).

a: góc EAF=90 độ, M là trung điểm của EF
=>MA=ME=MF
=>góc MAE=góc MEA
AC*AE=AD*AF
=>AC/AD=AF/AE
=>ΔACD đồng dạng với ΔAFE
=>góc ACD=góc AFE
AM cắt CD tại L
góc LCA+góc LAC=góc AEF+góc AFE=90 độ
=>AM vuông góc CD

a) góc MAN nội tiếp chắn nửa (O) => góc MAN = 900 hay góc CAD = 900
tam giác CAD vuông tại A có đường cao AB => AM.AC = AB2 = 4R2 không đổi
b) Tam giác OAN có OA = ON = R nên cân tại O => góc OAN = góc ONA hay góc BAD = góc MNA
mà góc BAD = góc ACD (cùng phụ góc BAC) => góc MNA = góc ACD => tứ giác CMND nội tiếp
c) tam giác ACD vuông tại A có AI là trung tuyến => IA = ID = 1/2 CD => tam giác IAD cân tại I => góc IAD = góc IDA
mà góc IDA = góc AMN( tứ giác CMND nội tiếp) => góc IAD = góc AMN mà góc AMD phụ góc MNA => góc IAD phụ góc MNA
=> góc AHN = 900 hay góc AHO = 900 , mà OA = R không đổi => H nằm trên đường tròn đường kính AO
a﴿ góc MAN nội tiếp chắn nửa ﴾O﴿ => góc MAN = 90o hay góc CAD = 90o
tam giác CAD vuông tại A có đường cao AB => AM.AC = AB 2 = 4R 2 không đổi
b﴿ Tam giác OAN có OA = ON = R nên cân tại O => góc OAN = góc ONA hay góc BAD = góc MNA
mà góc BAD = góc ACD ﴾cùng phụ góc BAC﴿ => góc MNA = góc ACD => tứ giác CMND nội tiếp
c﴿ tam giác ACD vuông tại A có AI là trung tuyến => IA = ID = 1/2 CD => tam giác IAD cân tại I => góc IAD = góc IDA
mà góc IDA = góc AMN﴾ tứ giác CMND nội tiếp﴿
=> góc IAD = góc AMN mà góc AMD phụ góc MNA => góc IAD phụ góc MNA
=> góc AHN = 90 0 hay góc AHO = 90 0 , mà OA = R không đổi => H nằm trên đường tròn đường kính AO



AC, AD cắt tiếp tuyến tại B.
mk viết nhầm