bài 1 : một tổ 10 bạn ngồi trong bàn tròn gồm 10 cái ghê , mỗi người ngồi một chỗ ngẫy nhiên , tính xác suất để ba và An ngồi cùng nhau
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 12 2020
Xếp A và B cạnh nhau: 2 cách
Coi cặp AB như 1 bạn, kết hợp 8 bạn còn lại, có \(9!\) cách hoán vị
Xác suất: \(P=\dfrac{9!.2}{10!}=\dfrac{1}{5}\)
CM
1 tháng 11 2019
Chọn A
Đánh số ba bàn tròn có số chỗ ngồi lần lượt là 6, 7, 8 là bàn 1, bàn 2, bàn 3.
+) Xét phép thử: “Xếp ngẫu nhiên 21 học sinh vào ba bàn tròn 1, 2, 3 nói trên”.
Chọn 6 học sinh trong số 21 học sinh và xếp vào bàn 1 có 
cách.
Chọn 7 học sinh trong số 15 học sinh còn lại và xếp vào bàn 2 có 
cách.
Xếp 8 học sinh còn lại vào bàn 3 có 7! cách.
Suy ra số phần tử của không gian mẫu là 
+) Gọi A là biến cố: “ Hai bạn Thêm và Quý luôn ngồi cạnh nhau ”.
Trường hợp 1: Hai bạn Thêm và Quý ngồi bàn 1.
Chọn 4 học sinh từ 19 học sinh còn lại có C 19 4 cách.
Xếp 4 học sinh vừa chọn và hai bạn Thêm, Quý vào bàn 1 có 4!.2! cách.
Chọn 7 học sinh từ 15 học sinh còn lại và xếp vào bàn 2 có 
cách.
Xếp 8 học sinh còn lại vào bàn 3 có 7! cách.
Số cách xếp thỏa mãn trường hợp 1 là: 
Trường hợp 2: Hai bạn Thêm và Quý ngồi bàn 2.
Tương tự như trên, ta có số cách xếp thỏa mãn trường hợp 2 là 
Trường hợp 3: Hai bạn Thêm và Quý ngồi bàn 3.
Tương tự như trên, ta có số cách xếp thỏa mãn trường hợp 3 là: 
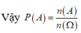
= C 19 4 . 4 ! . 2 ! . C 1 7 . 6 ! . 7 ! + C 19 5 . 5 ! . 2 ! . C 14 6 . 5 ! . 7 ! + C 19 6 . 6 ! . 2 ! . C 13 6 . 5 ! . 6 ! C 21 6 . 5 ! . C 15 7 . 6 ! . 7 ! = 1 10
CM
16 tháng 9 2018
Chọn B.
Kí hiệu học sinh lớp 12A, 12B, 12C lần lượt là A, B, C.
Số phần tử không gian mẫu là n(Ω)=9!
Gọi E là biến cố các học sinh cùng lớp luôn ngồi cạnh nhau. Ta có các bước sắp xếp như sau:
- Xếp 5 học sinh lớp 12C ngồi vào bàn sao cho các học sinh này ngồi sát nhau. Số cách sắp xếp là 5!
- Xếp 3 học sinh lớp 12B vào bàn sao cho các học sinh này ngồi sát nhau và sát nhóm của học sinh 12C. Số cách sắp xếp là 3!.2
- Xếp 2 học sinh lớp 12A vào hai vị trí còn lại của bàn. Số cách sắp xếp là 2!
Số phần tử thuận lợi cho biến cố E là n(E)=5!.3!.2.2!
Xác suất của A là P ( E ) = n ( E ) n ( Ω ) = 1 126
24 tháng 8 2016
xếp ngẫu nhiên 8 bạn học sinh vào 4 bàn có 8! cách 40320 cách
=> \(n\left(\Omega\right)=40320\)
Gọi A:" có đúng 2 bàn mà trong đó mỗi bàn gồm 1 nam và 1 nữ "
=> \(n\left(A\right)=C^1_4.C^1_4..4.C^1_3.C^1_3.3.C^2_2.2.C^2_2.1=3456\) cách
=> P(A)= 3456/40320 =3/35
H
26 tháng 5 2023
Kí hiệu tắt ông là M và bà là W. Không gian mẫu E có \(6!=720\) (phần tử).
1.
Có 2 cách xếp người cùng phái ngồi gần nhau: \(MMMWWW,WWWMMM\).
Có \(3!=6\) cách ngồi của 3 ông và có \(3!=6\) cách ngồi của 3 bà.
Vậy xác suất phải tính là \(P=\dfrac{2.3!.3!}{6!}=\dfrac{1}{10}\)
2.
Có 4 cách sắp xếp 3 bà ngồi gần nhau: \(MMMWWW,MMWWWM,MWWWMM,WWWMMM\).
Có \(3!=6\) cách sắp xếp 3 ông và có \(3!=6\) cách sắp xếp 3 bà.
Vậy xác suất phải tính là \(P=\dfrac{4.3!.3!}{6!}=\dfrac{1}{5}\).
3.
Có 2 cách sắp xếp 3 ông và 3 bà ngồi xen kẽ nhau: \(MWMWMW,WMWMWM.\)
Có \(3!=6\) cách sắp xếp 3 ông và có \(3!=6\) cách sắp xếp 3 bà.
Vậy xác suất phải tính là \(P=\dfrac{2.3!.3!}{6!}=\dfrac{1}{10}\)
CM
3 tháng 12 2018
Chọn đáp án A
Kí hiệu Nam: l và Nữ: ¡. Ta có
Có 2 trường hợp Nam, nữ ken kẽ nhau và 4 trường hợp hai bạn Nữ ngồi cạnh nhau.
Trường hợp 1. Nam nữ ngồi xen kẽ nhau gồm:
Nam phía trước: l¡l¡l¡l¡l¡.
Nữ phía trước: ¡l¡l¡l¡l¡l.
Trường hợp 2. Hai bạn nữ ngồi cạnh nhau: l¡¡l¡l¡l¡l Hoặc
l¡l¡¡l¡l¡l. Tương tự ta có thêm 2 trường hợp nữa. Các bước xếp như sau:
B1: Xếp 5 bạn nam. B2: Xếp cặp Tự - Trọng. B3: Xếp các bạn nữ còn lại. Khi đó số kết quả xếp cho 2 trường hợp trên như sau:
số cách ngồi của 10 người là: \(\)v=10!
gọi A là biến cố " Ba và An ngồi cạnh nhau"
ta có :
số cách xếp chỗ An là 10 cách
số cách xếp chỗ Ba là 2 cách ( vì 2 bạn ngồi cạnh nhau)
số cách xếp cho 8 người còn lại là :8!
=> số cách Ba và An ngồi cạnh nhau là : 10.2.8!=20.8!
=> n(A)=20.8!=> P(A)=\(\frac{20.8!}{10!}=\frac{20}{9.10}=\frac{2}{9}\)