Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
Số phần tử của không gian mẫu: n ( Ω ) = 5!
Gọi A:”Hai bạn An và Bình không ngồi cạnh nhau”
Thì A ¯ :”Hai bạn An và Bình ngồi cạnh nhau”
Xếp An và Bình ngồi cạnh nhau coi như 1 phần tử
- Xếp 1 phần tử (An+Bình) và 3 bạn còn lại theo các thứ tự khác nhau có: 4! Cách
- Xếp 2 học sinh An và Bình ngồi cạnh nhau có 2! cách
Suy ra 
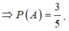

Chọn A
Đánh số ba bàn tròn có số chỗ ngồi lần lượt là 6, 7, 8 là bàn 1, bàn 2, bàn 3.
+) Xét phép thử: “Xếp ngẫu nhiên 21 học sinh vào ba bàn tròn 1, 2, 3 nói trên”.
Chọn 6 học sinh trong số 21 học sinh và xếp vào bàn 1 có ![]() cách.
cách.
Chọn 7 học sinh trong số 15 học sinh còn lại và xếp vào bàn 2 có ![]() cách.
cách.
Xếp 8 học sinh còn lại vào bàn 3 có 7! cách.
Suy ra số phần tử của không gian mẫu là ![]()
+) Gọi A là biến cố: “ Hai bạn Thêm và Quý luôn ngồi cạnh nhau ”.
Trường hợp 1: Hai bạn Thêm và Quý ngồi bàn 1.
Chọn 4 học sinh từ 19 học sinh còn lại có C 19 4 cách.
Xếp 4 học sinh vừa chọn và hai bạn Thêm, Quý vào bàn 1 có 4!.2! cách.
Chọn 7 học sinh từ 15 học sinh còn lại và xếp vào bàn 2 có ![]() cách.
cách.
Xếp 8 học sinh còn lại vào bàn 3 có 7! cách.
Số cách xếp thỏa mãn trường hợp 1 là: ![]()
Trường hợp 2: Hai bạn Thêm và Quý ngồi bàn 2.
Tương tự như trên, ta có số cách xếp thỏa mãn trường hợp 2 là ![]()
Trường hợp 3: Hai bạn Thêm và Quý ngồi bàn 3.
Tương tự như trên, ta có số cách xếp thỏa mãn trường hợp 3 là: ![]()
![]()
![]()
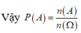
= C 19 4 . 4 ! . 2 ! . C 1 7 . 6 ! . 7 ! + C 19 5 . 5 ! . 2 ! . C 14 6 . 5 ! . 7 ! + C 19 6 . 6 ! . 2 ! . C 13 6 . 5 ! . 6 ! C 21 6 . 5 ! . C 15 7 . 6 ! . 7 ! = 1 10

a) Có 2. 9 = 18 cách xếp chỗ cho An và Bình ngồi cạnh nhau.
8 bạn kia được xếp vào 8 chỗ còn lại. Vậy có 8! cách xếp 8 bạn còn lại và do đó có 18! 8 cách xếp sao cho An, Bình ngồi cạnh nhau.
b) Có 10! cách xếp chỗ ngồi cho 10 bạn.
Từ đó có 10! - 18. 8! = 72. 8! cách xếp chỗ cho 10 bạn mà An và Bình không ngồi cạnh nhau.

Chọn C
Số cách chọn của An là
C
10
3
; số cách chọn của Bình là
C
10
3
. Vậy số phần tử của không gian mẫu là: ![]()
Gọi A là biến cố “ Hai bộ ba số An và Bình chọn ra có nhiều nhất một số giống nhau”.
TH1: Không có số nào giống nhau thì có C 10 3 C 7 3 cách chọn.
TH2: Có một số giống nhau thì có C 10 3 C 3 1 C 7 2 cách chọn.
Do đó ![]()
Vậy xác suất cần tìm là:
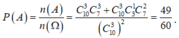

1.
Không gian mẫu: \(8!\)
Xếp Quân Lâm cạnh nhau: \(2!\) cách
Coi cặp Quân-Lâm như 1 bạn, hoán vị với 6 bạn còn lại: \(7!\) cách
\(\Rightarrow2!.7!\) cách xếp thỏa mãn
Xác suất: \(P=\dfrac{2!.7!}{8!}=\dfrac{1}{4}\)
2.
Không gian mẫu: \(C_{12}^3\)
Lấy 3 bóng sao cho ko có bóng tốt nào (cả 3 đều là bóng ko tốt): \(C_4^3\) cách
\(\Rightarrow C_{12}^3-C_4^3\) cách lấy 3 bóng sao cho có ít nhất 1 bóng tốt
Xác suất: \(P=\dfrac{C_{12}^3-C_4^3}{C_{12}^3}=...\)
3.
Số tam giác bằng với số cách chọn 3 điểm từ 4 điểm nên có: \(C_4^3=...\) tam giác
4.
\(T_{\overrightarrow{v}}\left(E\right)=F\left(x;y\right)\Rightarrow\left\{{}\begin{matrix}x=-3+1=-2\\y=5-2=3\end{matrix}\right.\) \(\Rightarrow\left(-2;3\right)\)
5.
Có 2 cạnh chéo nhau với AB là SC, SD
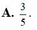
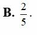
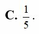
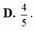


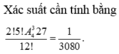

Xếp A và B cạnh nhau: 2 cách
Coi cặp AB như 1 bạn, kết hợp 8 bạn còn lại, có \(9!\) cách hoán vị
Xác suất: \(P=\dfrac{9!.2}{10!}=\dfrac{1}{5}\)