phan tích đa thức thành nhân tử: (x2+y2)3 + (z2 - x2)3 - (y2+z2)3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1. Ta có: hằng đẳng thức: \(x^3+y^3+z^3=3xyz\) nếu x+y+z=0
đặt b-c=x, c-a=y, a-b=z⇒x+y+z=0
\(\Rightarrow\left(b-c\right)^3+\left(c-a\right)^3+\left(a-b\right)^3=3\left(a-b\right)\left(c-a\right)\left(b-c\right)\)
2. \(x^3+y^3+z^3-3xyz=\left(x+y+z\right)\left(x^2+y^2+z^2-xy-yz-zx\right)+3xyz-3xyz=\left(x+y+z\right)\left(x^2+y^2+z^2-xy-yz-zx\right)\)
3. Tham khảo: https://hoc247.net/hoi-dap/toan-8/phan-tich-da-thuc-x-y-5-x-5-y-5-thanh-nhan-tu-faq447273.html
\(5,=x^3+2x^2y-7x^2y-14xy^2\\ =x^2\left(x+2y\right)-7xy\left(x+2y\right)\\ =x\left(x-7y\right)\left(x+2y\right)\)


x 2 y + x y 2 + x 2 z + x z 2 + y 2 z + y z 2 + 3xyz.
= ( x 2 y + x 2 z + xyz) + (x y 2 + y 2 z + xyz) + (x z 2 + y z 2 + xyz)
= x(xy + xz + yz) + y(xy + yz + xz) + z(xz + yz + xy)
= (x + y + z)(xy + xz + yz).
\(x^2y+xy^2+x^2z+xz^2+y^2z+yz^2+3xyz\)
\(=\left(x^2y+x^2z+xyz\right)+\left(xz^2+yz^2+xyz\right)+\left(xy^2+y^2z+xyz\right)\)
\(=x\left(xy+xz+yz\right)+z\left(xz+yz+xy\right)+y\left(xy+yz+xz\right)\)
\(=\left(x+y+z\right)\left(xy+yz+xz\right)\)

b: \(x^2-2xy+y^2-z^2\)
\(=\left(x-y\right)^2-z^2\)
\(=\left(x-y-z\right)\left(x-y+z\right)\)
d: \(x^2+4x+3=\left(x+3\right)\left(x+1\right)\)

\(=\left(x^2-2x+1\right)-\left(y^2-2yz+z^2\right)\)
\(=\left(x-1\right)^2-\left(y-z\right)^2\)
\(=\left(x-1-y+z\right)\left(x-1+y-z\right)\)
\(x^2-2x+1-y^2+2yz-z^2\)
\(=\left(x-1\right)^2-\left(y-z\right)^2\)
\(=\left(x-1-y+z\right)\left(x-1+y-z\right)\)

x2 – 2xy + y2 – z2 + 2zt – t2
(Nhận thấy x2 – 2xy + y2 và z2 – 2zt + t2 là các hằng đẳng thức)
= (x2 – 2xy + y2) – (z2 – 2zt + t2)
= (x – y)2 – (z – t)2 (xuất hiện hằng đẳng thức (3))
= [(x – y) – (z – t)][(x – y) + (z – t)]
= (x – y – z + t)(x – y + z –t)

a: Ta có: \(x^2-xy-3x+3y\)
\(=x\left(x-y\right)-3\left(x-y\right)\)
\(=\left(x-y\right)\left(x-3\right)\)
b: Ta có: \(5x^2+5xy-x-y\)
\(=5x\left(x+y\right)-\left(x+y\right)\)
\(=\left(x+y\right)\left(5x-1\right)\)
c: Ta có: \(x^2-2xy+y^2-z^2\)
\(=\left(x-y\right)^2-z^2\)
\(=\left(x-y-z\right)\left(x-y+z\right)\)

\(1,\\ a,=\left(x-y\right)^2-z^2=\left(x-y-z\right)\left(x-y+z\right)\\ b,=a^2\left(a-x\right)-y\left(a-x\right)=\left(a^2-y\right)\left(a-x\right)\\ c,=\left(x-y\right)^2-z\left(x-y\right)=\left(x-y\right)\left(x-y-z\right)\\ d,=x\left(x-2y\right)+t\left(x-2y\right)=\left(x+t\right)\left(x-2y\right)\\ 2,\\ \Rightarrow x^2-4x+4-x^2+9=6\\ \Rightarrow-4x=-7\Rightarrow x=\dfrac{7}{4}\\ 3,\\ a,x^2+2x+2=\left(x+1\right)^2+1\ge1>0\\ b,-x^2+4x-5=-\left(x-2\right)^2-1\le-1< 0\)
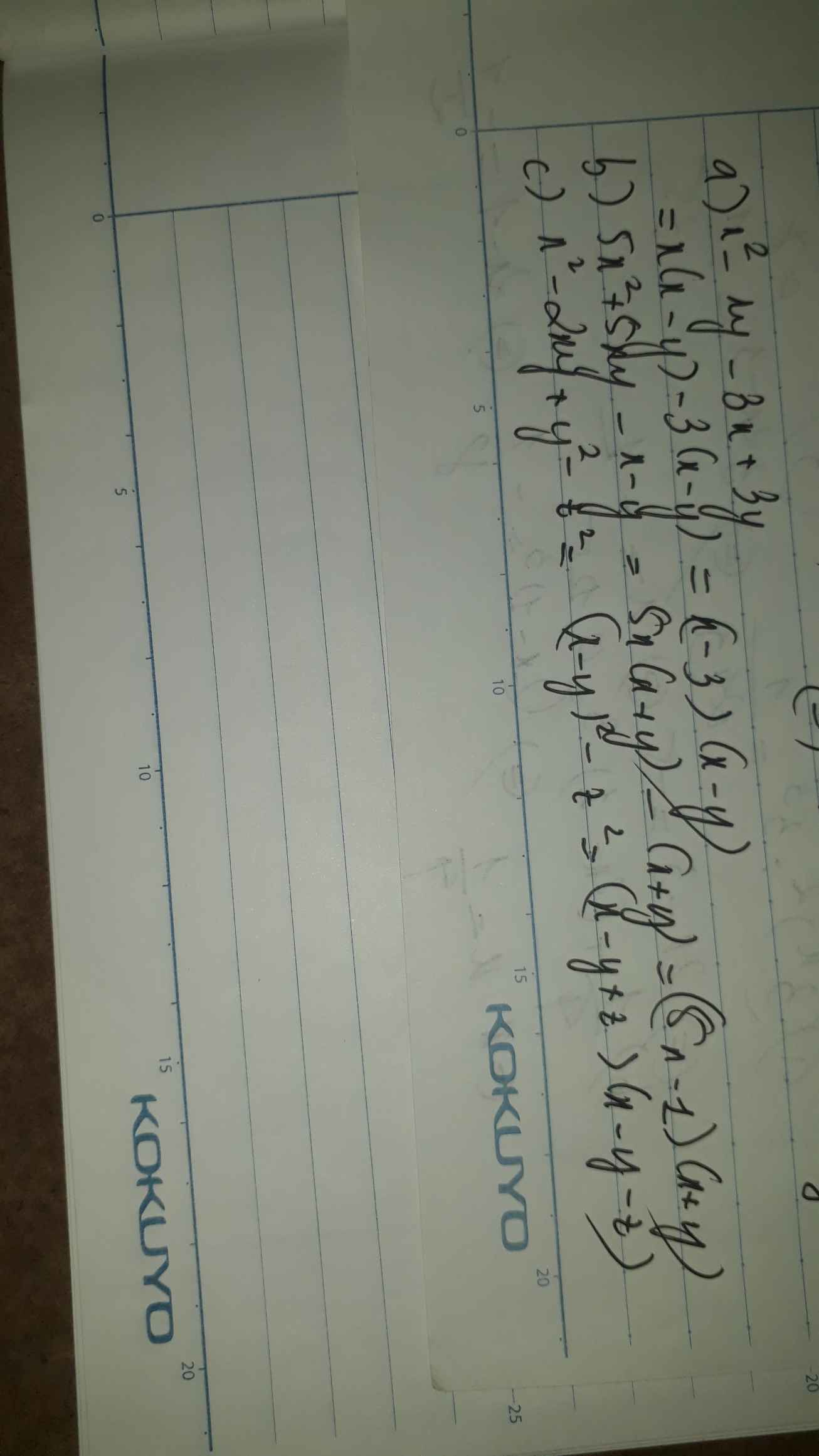
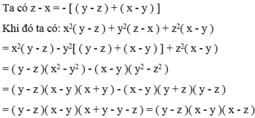
thanks nhìu