cho hình chóp SABCD có ABCD là hình vuông cạnh a. SA vuông với đáy . SA=2a . Gọi I là trung điểm SC . Tính V của IABCD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
19 tháng 9 2019
Chọn A.
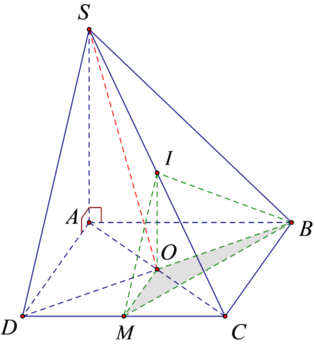
Do IO là đường trung bình của tam giác SAC nên:
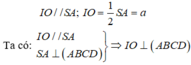
* OM là đường trung bình tam giác ACD nên:
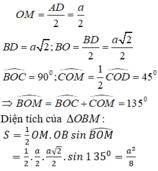
Tính thể tích của khối chóp I.OBM:
CM
25 tháng 4 2017
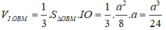
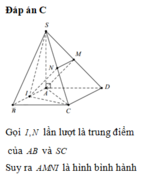
Đáp án C
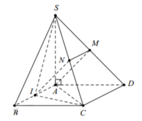
Gọi I;N lần lượt là trung điểm của AB và SC
Suy ra AMNI là hình bình hành ⇒ A M ∥ I N ⇒ A M ∥ S C I
Do đó d A M , S C = d A M , S C I = d A ; S C I = h
Kẻ A H ⊥ I C H ∈ I C , A K ⊥ S H K ∈ S H ⇒ A K ⊥ S C I
Ta có S Δ A C I = 1 2 S Δ A B C = 1 2 . A H . I C ⇒ A H = a 2 4 : a 5 4 = a 5 5
Tam giác SAH vuông tại A , có 1 A K 2 = 1 A H 2 + 1 S A 2 ⇒ A K = 2 a 21
Vậy khoảng cách cần tính là h = 2 a 21 21
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 6 2021
\(\dfrac{V_{SAHKE}}{V_{SABCD}}=\dfrac{2V_{SAHK}}{2V_{SABC}}=\dfrac{V_{SAHK}}{V_{SABC}}\)
\(V_{SABC}=\dfrac{1}{3}SA.\dfrac{1}{2}AB.BC=\dfrac{a^3}{3}\); \(V_{SABCD}=\dfrac{2a^3}{3}\)
\(\dfrac{SH}{SB}=\dfrac{SA^2}{SB}:SB=\left(\dfrac{SA}{SB}\right)^2\); \(\dfrac{SK}{SC}=\dfrac{SA^2}{SC}:SC=\left(\dfrac{SA}{SC}\right)^2\)
\(SB=\sqrt{SA^2+AB^2}=a\sqrt{5}\) ; \(SC=\sqrt{SA^2+AC^2}=a\sqrt{6}\)
\(\dfrac{V_{SAHK}}{V_{SABC}}=\left(\dfrac{SA}{SB}\right)^2.\left(\dfrac{SA}{SC}\right)^2\)
\(\Rightarrow V_{SAHKE}=\left(\dfrac{2a}{a\sqrt{5}}\right)^2.\left(\dfrac{2a}{a\sqrt{6}}\right)^2.\dfrac{2a^3}{3}=\dfrac{16a^3}{45}\)
QN
2 tháng 8 2023
Để tính thể tích SAPMQ, ta cần tìm độ dài đoạn PM và đoạn MQ. Gọi E là trung điểm của BD. Ta có ME song song với AM và ME = 1/2 BD = 1/2 a. Vì (∆) song song với BD nên góc AME = góc ABD = 45 độ. Vì SA vuông góc với ABCD nên góc SAM = 90 độ. Vì SA = a√3 và góc SAM = 90 độ nên tam giác SAM là tam giác vuông cân tại A. Do đó, góc ASM = 45 độ. Vì góc ASM = góc AME = 45 độ nên tam giác ASM và tam giác AME đồng dạng. Vậy, ta có: AM/AS = AE/AM AM^2 = AS * AE AM^2 = (a√3) * (1/2 a) AM^2 = a^2 * √3 / 2 AM = a√3 / √2 AM = a√6 / 2 Ta có ME = 1/2 a Vậy, PM = AM - ME = (a√6 / 2) - (1/2 a) = (a√6 - a) / 2 Tương tự, ta có MQ = AM + ME = (a√6 / 2) + (1/2 a) = (a√6 + a) / 2 Vậy, thể tích SAPMQ = SABC * PM = a^2 * (a√6 - a) / 2 = a^3√6 / 2 - a^3 / 2
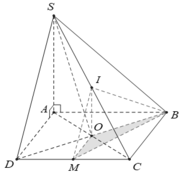
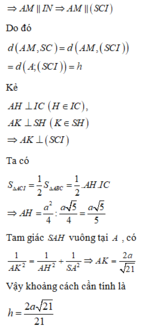
Dựa vào tỉ lệ thể tính ta có: \(\frac{VS.ABCD}{VI.ABCD}=\frac{VC.DSAB}{VC.DIAB}=\frac{CD}{CD}.\frac{CB}{CB}.\frac{CA}{CA}.\frac{CS}{CI}=2\) \(\Rightarrow VI.ABCD=\frac{VS.ABCD}{2}\) Mà VS.ABCD= \(\frac{1}{3}SA.SABCD=\frac{1}{3}\) 2a.\(a^2\) =\(\frac{2}{3}a^3\) Vậy VI.ABCD=\(\frac{1}{3}a^3\)
Thân chào.
Đối với câu hỏi này, theo mình đáp án đúng nhất là vận động xã hội. Thế nhưng, đáp án mà chương trình đưa ra là vận động sinh học.
Có thể giúp mình lí giải điều này được chứ?
Cảm ơn.