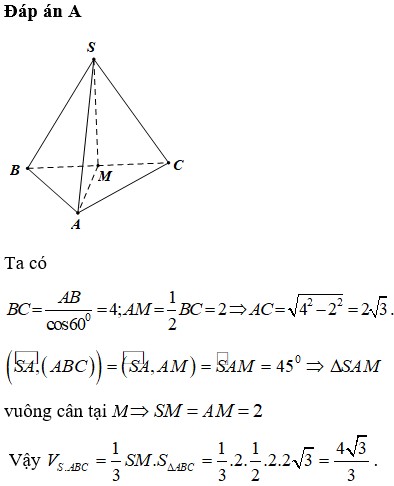
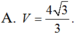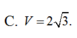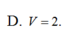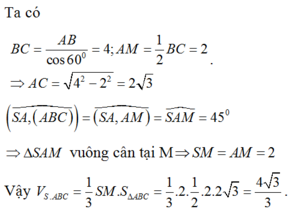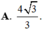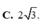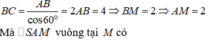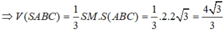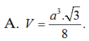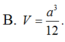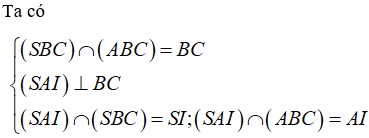cho hình chóp sabc có đáy abc là tam giác đều cạnh a. hình chiếu vuông góc của đỉnh s trên mặt đáy abc trùng với trung điểm h của trung tuyến ad. tính thể tích khối chóp sabc biết góc giữ sh và mp sbc là 30 độ.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 4 2021
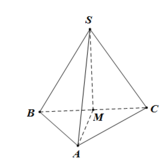
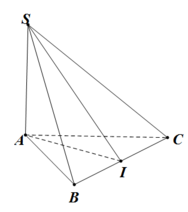
\(SH\perp\left(ABC\right)\Rightarrow\widehat{SAH}\) là góc giữa SA và (ABC)
\(SH=\dfrac{a\sqrt{3}}{2}\) (đường trung tuyến trong tam giác đều SBC cạnh a)
\(AH=\dfrac{a\sqrt{3}}{2}\) (đường trung tuyến trong tam giác đều ABC cạnh a)
\(tan\widehat{SAH}=\dfrac{SH}{AH}=1\Rightarrow\widehat{SAH}=45^0\)
CM
1 tháng 12 2017
Đáp án D
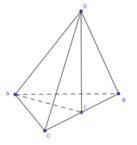
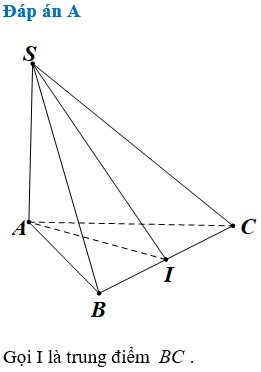
Góc giữa cạnh SA và đáy là SAF ,
Vì tam giác ABC và SBC là tam giác đều cạnh a nên ta có
A F = 3 2 a ; S F = 3 2 a
Vậy tan S A F ^ = 1 ⇒ S A G ^ = 45 0
18 tháng 11 2021
Cho hình chop SABC, có đáy là ABC là tam giác vuông tại B, có độ dài các cạch AB=6,BC=8,SA=10 vuông góc với mặt đáy Tính thể tích khối chóp SABC
BN
18 tháng 4 2016
chứng minh được AH=BH -> SA= SB _> tam giác SAB cân ở S
gọi M là trung điểm của AB -> SM vuông góc với AB -> góc giữa mp (SAB) và mp (ABC) là góc SMH -> góc SMH = 60 độ
-> tìm được SH -> tìm được thể tích
tìm diên tích tam giác SAB -> khoảng cách từ C đến mp (SAB)
Vì I là trung điểm của SC nên khoảng cách từ I đến mp (SAB) bằng một nửa khoảng cách từ C đến mp (SAB)