tìm các số nguyên a và b sao cho : a2-2ab+2b2-4a+7<0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Do a và b nguyên ta cộng 1 vào vế trái của BPT đã cho và được:
a2 -2ab + 2b2 - 4a + 8 < hoặc = 0
<=> 2a2 - 4ab + 4b2 - 8a + 16 < hoặc = 0
<=> ( a-2b)2 + (a-4)2 < hoặc = 0
Dấu "=" xảy ra khi :
a=4;b=2


Chọn đáp án B.
Bằng cách sử dụng điều kiện tồn tại nghiệm của phương trình, chúng ta có: Khi a = 0 thì hàm số chỉ đạt giá trị lớn nhất (khi b < 0) hoặc chỉ đạt giá trị nhỏ nhất (khi b > 0). Còn khi
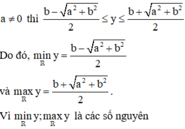
nên tập giá trị của hàm số đã cho chỉ có đúng 6 số nguyên khi và chỉ khi
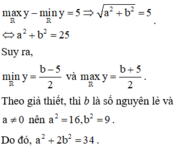

Lời giải:
$a^2-2ab-3b^2\geq 0$
$\Leftrightarrow (a^2+ab)-(3ab+3b^2)\geq 0$
$\Leftrightarrow a(a+b)-3b(a+b)\geq 0$
$\Leftrightarrow (a+b)(a-3b)\geq 0$
$\Leftrightarrow a-3b\geq 0$ (do $a+b>0$ với mọi $a,b>0$)
$\Leftrightarrow a\geq 3b$
Xét hiệu:
$P-\frac{37}{3}=\frac{4a^2+b^2}{ab}-\frac{37}{3}$
$=\frac{12a^2+3b^2-37ab}{3ab}=\frac{(a-3b)(12a-b)}{3ab}\geq 0$ do $a\geq 3b>0$
$\Rightarrow P\geq \frac{37}{3}$
Vậy $P_{\min}=\frac{37}{3}$

\(4x=7y\Rightarrow\dfrac{x}{7}=\dfrac{y}{4}\Rightarrow\dfrac{x^2}{49}=\dfrac{y^2}{16}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\dfrac{x^2}{49}=\dfrac{y^2}{16}=\dfrac{x^2+y^2}{49+16}=\dfrac{260}{65}=4\)
\(\Rightarrow\left\{{}\begin{matrix}x^2=196\\y^2=64\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=-14;y=-8\\x=14;y=8\end{matrix}\right.\)


Ta có : a2 + 2ab + b2 + b2 - 4b +4 = 0
<=> ( a + b )2 + ( b - 2 )2 = 0
mà: ( a + b )2≥0 ∀a,b
( b - 2 )2 ≥0 ∀b
Dấu "=" xảy ra khi :
a + b =0
b - 2 =0
<=> a + 2 =0 <=> a = -2
b =2
Thay a = -2 ; b =2 vào ta có:
M= 22 +7.2.2 + \(\dfrac{52}{-2-2}\)
M= 4 +28- \(\dfrac{52}{4}\)
M= 4 +28 - 13 = 19
Do a và b nguyên ta cộng 1 vào vế trái của BPT đã cho và được:
a2 -2ab + 2b2 - 4a + 8 < hoặc = 0
<=> 2a2 - 4ab + 4b2 - 8a + 16 < hoặc = 0
<=> ( a-2b)2 + (a-4)2 < hoặc = 0
Dấu "=" xảy ra khi :
a=4;b=2
Do a và b nguyên ta cộng 1 vào vế trái của BPT đã cho và được:
a2 -2ab + 2b2 - 4a + 8 < hoặc = 0
<=> 2a2 - 4ab + 4b2 - 8a + 16 < hoặc = 0
<=> ( a-2b)2 + (a-4)2 < hoặc = 0
Dấu "=" xảy ra khi :
a=4;b=2