Hình vuông ABCD có A(1;-3), B(5;4). Tìm tọa độ các đỉnh còn lại ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 10 2023
Xét dãy số \(u_n=S_{A_nB_nC_nD_n}\). Ta có \(u_1=a^2\)
Ta xét hình vuông có cạnh \(x\) (diện tích là \(x^2\)). Khi đó nửa độ dài đường chéo của hình vuông này sẽ là \(\dfrac{x}{\sqrt{2}}\). Khi đó diện tích của hình vuông mới là \(\left(\dfrac{x}{\sqrt{2}}\right)^2=\dfrac{x^2}{2}\) bằng 1 nửa diện tích hình vuông ban đầu. Như vậy, ta có mối quan hệ truy hồi: \(u_{n+1}=2u_n\). Dễ thấy đây là một cấp số nhân.
Ta có \(\left(u_n\right):\left\{{}\begin{matrix}u_1=a^2\\u_{n+1}=2u_n\end{matrix}\right.\)
\(\Rightarrow S_n=\sum\limits^{\infty}_{i=1}u_i=a^2\left(\sum\limits^{\infty}_{i=0}\dfrac{1}{2^i}\right)=2a^2\)
(Đẳng thức quen thuộc \(\sum\limits^{\infty}_{i=0}\dfrac{1}{2^i}=2\))
Cho \(S_n=8\) \(\Rightarrow2a^2=8\Leftrightarrow a=2\).
Vậy \(a=2\) thỏa mãn ycbt.
12 tháng 2 2019
a,Diện tích hình vuông ABCD là:
48 x 3 = 144 (cm2)
Ta có 12 x 12 = 144
Chu vi hình ABCD là
12 x 4 = 48 (cm)
b,Diện tích hình chữ nhật đó là
144 : 9 x 8 = 128(cm2)
Tổng của chiều dài và chiều rộng là
48 : 2 = 24 (cm)
Vậy hai số có tổng là 24 và tích là 128 là 16 và 8
Đáp số:a,48 cm
b,Chiều dài:16
Chiều rộng:8
22 tháng 9 2023
a) 48cm2 trong đề bài tương ứng với diện tích của phần được mở rộng, gồm chiều dài là chiều dài hình vuông và chiều rộng là 1/3 chiều dài hình vuông. Do đó chiều dài hình vuông nhân với chính nó, hay diện tích hình vuông là:
48 : 1/3 = 144 (cm2)
Vì 12 x 12 = 144 nên chiều dài hình vuông là 12cm.
Chu vi hình vuông là:
12 x 4 = 48 (cm)
b) Diện tích của hình chữ nhật đó là:
144 x 8/9 = 128(cm2)
Nửa chu vi của hình chữ nhật đó là:
48 : 2 = 24 (cm)
Do đó chiều dài và chiều rộng lần lượt là hai số tự nhiên a và b sao cho a + b = 24 và a x b = 128.
Dễ thấy a = 24 - b = 128 : b, suy ra b = 8, a = 24 - 8 = 16.
Vậy chiều dài và chiều rộng của hình chữ nhật đó lần lượt là 16cm và 8cm.
10 tháng 5 2023
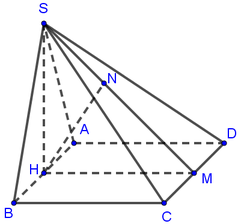
1: CD vuông góc AD
CD vuông góc SA
=>CD vuông góc (SAD)
=>(SCD) vuông góc (SAD)
25 tháng 1 2022
a) cạnh hình vuông MNPQ là 3x2=6(cm)
Chu vi MNPQ là 4x6=24
b) =1/3 nha
chúc bạn hoc tốt
HYC-25/1/2022
25 tháng 1 2022
Cạnh hình vuông MNPQ :
2 x 3 = 6 ( cm )
Chu vi MNPQ :
4 X 6 = 24 ( cm )
b. 1/3
HT
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 3 2023
Do ABCD là hình vuông \(\Rightarrow AB=d\left(A;BC\right)=\dfrac{\left|0-2.2-1\right|}{\sqrt{1^2+\left(-2\right)^2}}=\sqrt{5}\)
\(\Rightarrow AC=AB\sqrt{2}=\sqrt{10}\)
Do C thuộc BC \(\Rightarrow C\left(2c+1;c\right)\) \(\Rightarrow\overrightarrow{AC}=\left(2c+1;c-2\right)\)
\(\Rightarrow AC^2=\left(2c+1\right)^2+\left(c-2\right)^2=10\)
\(\Leftrightarrow5c^2-5=0\Rightarrow\left[{}\begin{matrix}c=1\\c=-1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}C\left(3;1\right)\\C\left(-1;-1\right)\end{matrix}\right.\)
Do C có hoành độ dương \(\Rightarrow C\left(3;1\right)\)
N là trung điểm AC \(\Rightarrow N\left(\dfrac{3}{2};\dfrac{3}{2}\right)\)
1 tháng 8 2017
a]Hình chữ nhật ABCD co16 ovuong.
b]Hình tam giác EDC có 4 ô vuông
c]Số ô vuông ABCD gấp 4 lần số o vuông của tam giác ECD.
đ]số ô vuông của tam giác EDC bằng 1/4 số ô vuông ABCD .
Ta có \(\overrightarrow{AB}\left(4;7\right)\) và \(\left|\overrightarrow{AB}\right|=AB=\sqrt{65}\)
Giả sử tìm được D(x;y), suy ra \(\overrightarrow{AD}=\left(x-1;y+3\right)\)
Do DA=AB và \(DA\perp AB\) nên
\(\begin{cases}4\left(x-1\right)+7\left(y+3\right)=0\\\left(x-1\right)^2+\left(y+3\right)^2=65\end{cases}\)
Giải hệ thu được \(\left(x;y\right)=\left(-6;1\right),\left(8;-7\right)\)
Vậy với D(-6;1) ta thu được C(-2;8);
Với D(8;-7) ta thu được C(12;0)