Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Diện tích hình vuông ban đầu bằng 1.1 = 1 (đvdt)
Vì người ta nối các trung điểm của cạnh hình vuông để tạo ra hình vuông mới nên diện tích hình mới sẽ bằng một nửa hình trước.
Do đó ta có \({u_1} = {S_1} = 1,q = \frac{1}{2}\)
Vậy \({S_n} = 1.\frac{{1 - {{\left( {\frac{1}{2}} \right)}^n}}}{{1 - \frac{1}{2}}} = {\left( {\frac{1}{2}} \right)^{n - 1}}\)
b) \(S = \frac{1}{{1 - \frac{1}{2}}} = 2\)

Đáp án B.
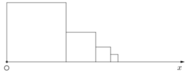
Tổng các cạnh nằm trên tia Ox của các canh hình vuông đó là:

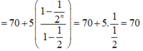

a.Gọi độ dài cạnh hình vuông là a thì diện tích hình vuông là: S = a2
Cạnh hình vuông kế tiếp bằng một nửa cạnh hình vuông trước đó
⇒ Diện tích hình vuông kế tiếp bằng một phần tư diện tích hình vuông trước đó.
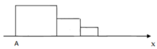
Hình vuông đầu tiên có độ dài cạnh là 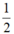 ( là hình vuông nhỏ được đánh số 1) nên có diện tích là:
( là hình vuông nhỏ được đánh số 1) nên có diện tích là: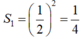
Từ đó , ta có:
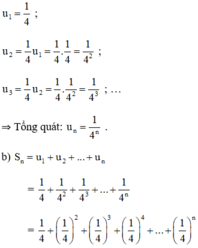
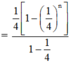 (Tổng của n số hạng đầu của CSN)
(Tổng của n số hạng đầu của CSN)
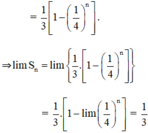

Đáp án C
Gọi H, K lần lượt là hình chiếu vuông góc của A, D lên EF ta có
![]()
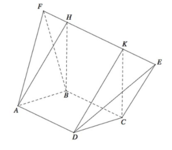
![]()
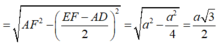
Vì vậy
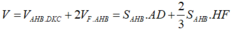
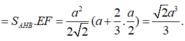

Chọn B
Tổng các cạnh nằm trên tia Ax của các hình vuông đó là
10 + 5 + 5 2 + 5 2 2 + . . . = 20 ( c m )

Đáp án B
Giả sử hình vuông ABCD có độ dài cạnh a.
Kẻ các đường sinh AH,BK ta có
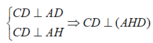
![]()
Theo pitago ta có
![]()
![]()
![]()
![]()

Đáp án C
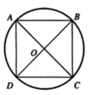
Do hình trụ và hình lập phương có cùng chiều cao nên ta chỉ cần chú ý đến mặt đáy như hình vẽ bên. Đường tròn đáy của hình trụ có bán kính bằng một nửa đường chéo của hình vuông
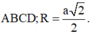 Do đó thể tích hình trụ cần tìm bằng
Do đó thể tích hình trụ cần tìm bằng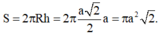

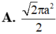
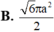

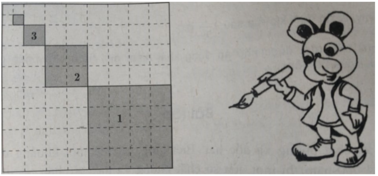
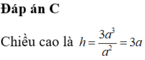
Xét dãy số \(u_n=S_{A_nB_nC_nD_n}\). Ta có \(u_1=a^2\)
Ta xét hình vuông có cạnh \(x\) (diện tích là \(x^2\)). Khi đó nửa độ dài đường chéo của hình vuông này sẽ là \(\dfrac{x}{\sqrt{2}}\). Khi đó diện tích của hình vuông mới là \(\left(\dfrac{x}{\sqrt{2}}\right)^2=\dfrac{x^2}{2}\) bằng 1 nửa diện tích hình vuông ban đầu. Như vậy, ta có mối quan hệ truy hồi: \(u_{n+1}=2u_n\). Dễ thấy đây là một cấp số nhân.
Ta có \(\left(u_n\right):\left\{{}\begin{matrix}u_1=a^2\\u_{n+1}=2u_n\end{matrix}\right.\)
\(\Rightarrow S_n=\sum\limits^{\infty}_{i=1}u_i=a^2\left(\sum\limits^{\infty}_{i=0}\dfrac{1}{2^i}\right)=2a^2\)
(Đẳng thức quen thuộc \(\sum\limits^{\infty}_{i=0}\dfrac{1}{2^i}=2\))
Cho \(S_n=8\) \(\Rightarrow2a^2=8\Leftrightarrow a=2\).
Vậy \(a=2\) thỏa mãn ycbt.