quy đồng mẫu thức của các phân tử
a, \(\dfrac{2}{5x^3y};\dfrac{5}{xy^2}\)
b, \(\dfrac{3x}{x-5};\dfrac{-2}{3\left(x-5\right)}\)
c, \(\dfrac{1}{\left(x+3\right)\left(x-3\right)};\dfrac{5x}{x^2-9}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TC
Trên con đường thành công không có....
28 tháng 7 2021
Đúng(2)
Những câu hỏi liên quan
7 tháng 12 2021
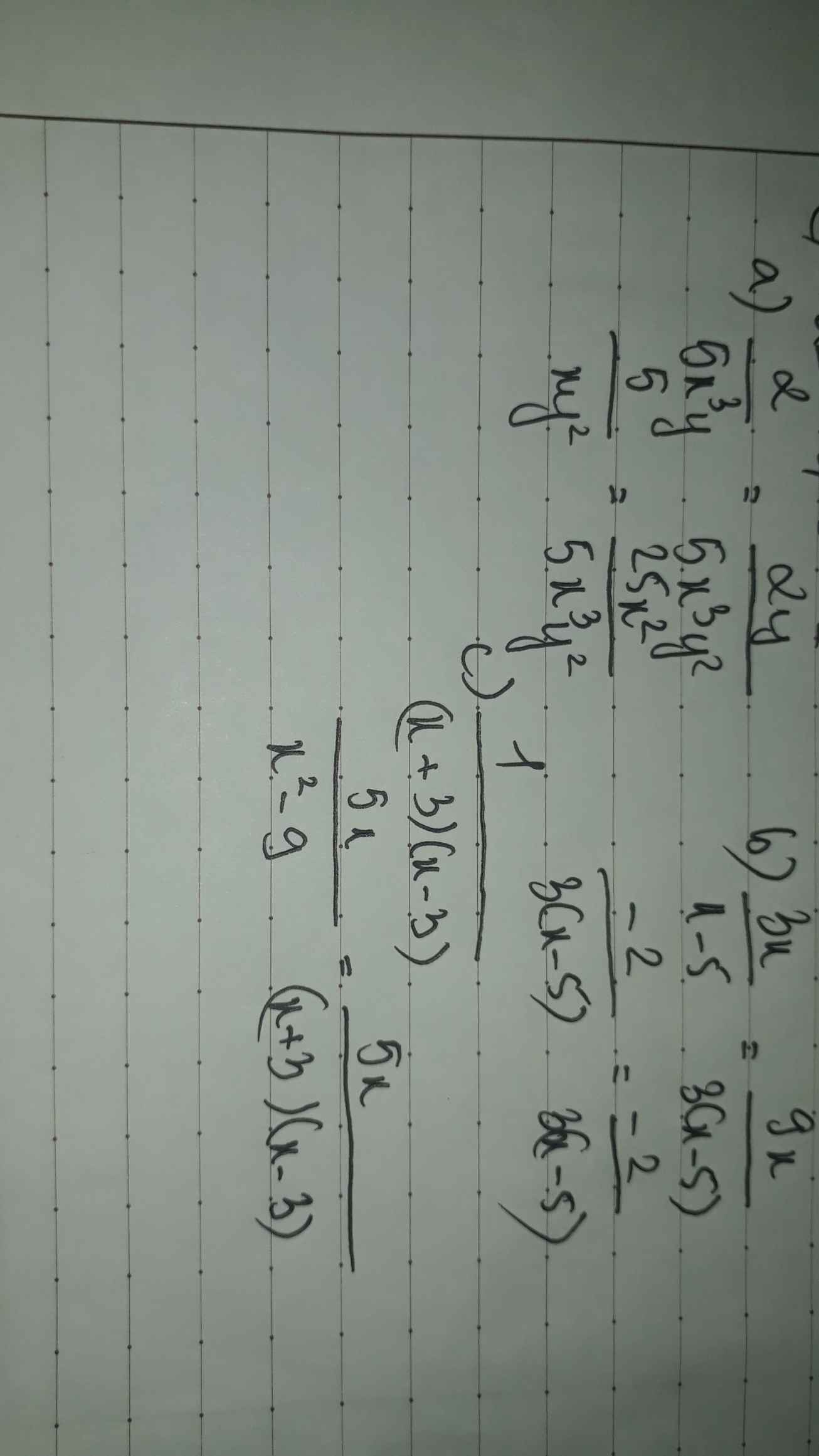
Bài 2:
a: \(\dfrac{1}{2x^3y}=\dfrac{6yz^3}{12x^3y^2z^3}\)
\(\dfrac{2}{3xy^2z^3}=\dfrac{2\cdot4x^2}{12x^3y^2z^3}=\dfrac{8x^2}{12x^3y^2z^3}\)
17 tháng 2 2021
a) MTC: \(12x^3y^3\)
\(\dfrac{3}{4x^3y^2}=\dfrac{3\cdot3y}{4x^3y^2\cdot3y}=\dfrac{9y}{12x^3y^3}\)
\(\dfrac{2}{3xy^3}=\dfrac{2\cdot4x^2}{3xy^3\cdot4x^2}=\dfrac{8x^2}{12x^3y^3}\)
b) MTC: \(x\left(x-3\right)^2\)
\(\dfrac{5}{x^2-6x+9}=\dfrac{5}{\left(x-3\right)^2}=\dfrac{5x}{x\left(x-3\right)^2}\)
\(\dfrac{3}{x^2-3x}=\dfrac{3}{x\left(x-3\right)}=\dfrac{3\left(x-3\right)}{x\left(x-3\right)^2}=\dfrac{3x-9}{x\left(x-3\right)^2}\)
PH
12 tháng 11 2017
a)MTC:\(12x^5y^4\)
\(\dfrac{5}{x^5y^3}=\dfrac{5\cdot12y}{x^5y^3\cdot12y}=\dfrac{60y}{12x^5y^4}\)
\(\dfrac{7}{12x^3y^4}=\dfrac{7\cdot x^2}{12x^3y^4\cdot x^2}=\dfrac{7x^2}{12x^5y^4}\)
b)MTC:\(60x^4y^5\)
\(\dfrac{4}{15x^3y^5}=\dfrac{4\cdot4x}{15x^3y^5\cdot4x}=\dfrac{16x}{60x^4y^5}\)
\(\dfrac{11}{12x^4y^2}=\dfrac{11\cdot5y^3}{12x^4y^2\cdot5y^3}=\dfrac{55y^3}{60x^4y^5}\)
21 tháng 4 2017
*Muốn quy đồng mẫu thức nhiều phân thức ta làm như sau:
-Phân tích các mẫu thức thành nhân tử rồi tìm ẫu tức chung.
-Tìm nhân tử phụ của mỗi mẫu thức.
-Nhân cả tử và mẫu của mỗi phân thức với nhân tử phụ tương ứng.
*Bài tập:
\(\dfrac{x}{x^2+2x+1}và\)\(\dfrac{3}{5x^2-5}\)
-Ta có:
x2+2x+1=(x+1)2=(x+1)(x+1)
5x2-5=5(x2-1)=5(x-1)(x+1)
\(\Rightarrow\)MTC:5(x-1)(x+1)(x+1)
-NTP:5(x-1)(x+1)(x+1):(x+1)(x+1)=5(x-1)
5(x-1)(x+1)(x+1):5(x-1)(x+1)=x+1
-Quy đồng mẫu thức:
\(\dfrac{x}{\left(x+1\right)\left(x+1\right)}\)=\(\dfrac{5x\left(x-1\right)}{5\left(x-1\right)\left(x+1\right)\left(x+1\right)}\)
\(\dfrac{3}{5\left(x-1\right)\left(x+1\right)}=\dfrac{3\left(x+1\right)}{5\left(x-1\right)\left(x+1\right)\left(x+1\right)}\)
11 tháng 12 2020
a) \(MTC=a^2x^2b^2\)
\(NTP:a^2x^2b^2:a^2x=xb^2\)
\(a^2x^2b^2:x^2b=a^2b\)
\(a^2x^2b^2:b^2a=ax^2\)
Quy đồng :
\(\dfrac{a+x}{a^2x}=\dfrac{\left(a+x\right)\cdot xb^2}{a^2x.xb^2}=\dfrac{axb^2+x^2b^2}{a^2x^2b^2}\)
\(\dfrac{a+b}{x^2b}=\dfrac{\left(a+b\right)\cdot a^2b}{x^2b\cdot a^2b}=\dfrac{a^3b+a^2b^2}{a^2x^2b^2}\)
\(\dfrac{b+a}{b^2a}=\dfrac{\left(b+a\right)\cdot ax^2}{b^2a\cdot ax^2}=\dfrac{abx^2+a^2x^2}{a^2x^2b^2}\)