Cho tam giác ABC có . Các đường trung trực của AB và AC cắt nhau tại I. Khi...
Đọc tiếp
Cho tam giác ABC có .
Các đường trung trực của AB và AC cắt nhau tại I.
Khi đó
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
DT
0
Những câu hỏi liên quan
TQ
0
CM
17 tháng 2 2019
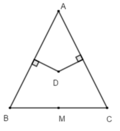
D là giao điểm của hai đường trực của hai cạnh AB và AC nên D là giao của ba đường trung trực trong tam giác ABC
Suy ra D thuộc đường trung trực của đoạn thẳng BC (1)
Lại có M là trung điểm của BC nên AM là trung tuyến của tam giác ABC cân tại A
Do đó AM là đường trung trực của BC (trong tam giác cân, trung tuyến tại đỉnh đồng thời cũng là đường trung trực ứng với đáy) (2)
Từ (1) và (2) suy ra A, D, M thẳng hàng nên A đúng.
Do tam giác ABC cân nên giao điểm D của ba đường trung trực của tam giác ABC không thuộc các đường thẳng AB, AC, BC nên B, C, D sai.
Chọn đáp án A
14 tháng 5 2023
Vì các đường trung trực của `\Delta ABC` cắt nhau tại điểm O
`->` `\text {AO}` là đường trung trực thứ `3` của `\Delta`
Xét các đáp án trên `-> D.`
CM
19 tháng 3 2017
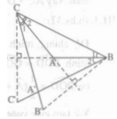
+) Vì AC là đường trung trực của BB'
Suy ra: CB’ =CB ( tính chất đường trung trực)
Do đó,tam giác CBB’ là tam giác cân tại C. Có CA là đường trung trực của BB’ nên đồng thời là đường phân giác nên có ∠C1= ∠C2.
+) Vì AB là đường trung trực của CC' nên BC = BC’.
Suy ra, tam giác BCC’ cân tại B. Lại có BA là đường trung trực nên đồng thời là đường phân giác (tính chất tam giác cân).
Suy ra: ∠B1 = ∠B2 .
+) Ta có: AB, AC lần lượt là đường phân giác của các góc A'BC và góc A'CB; hai đường này cắt nhau tại A.
Vậy ba đường phân giác của tam giác A'BC đồng quy tại A, hay A là điểm nằm trong tam giác A'BC và cách đều ba cạnh của tam giác này.
14 tháng 5 2022
giúp mình nhanh với , với vẽ hình cho mình luôn nha cảm ơn trước
TT
9 tháng 6 2020
Câu 1.
Gọi DI là trung trực BC
Xét ΔBIDvà ΔCID:
IDchung
\(\widehat{BDI}=\widehat{CDI}=90^o\)(ID trung trực BC)
BD = CD(như trên)
⇒ΔBID = ΔCID (c.g.c )
⇒ \(\widehat{IBD}=\widehat{C}\)(2gtu)
\(\widehat{B}-\widehat{C}\) = 40
hay \(\widehat{B}-\widehat{IBD}\) = 40
Mà\(\widehat{IBD}+\widehat{ABI}=B\)
\(\Rightarrow\widehat{ABI}=\widehat{B}-\widehat{IBD}=40^o\)