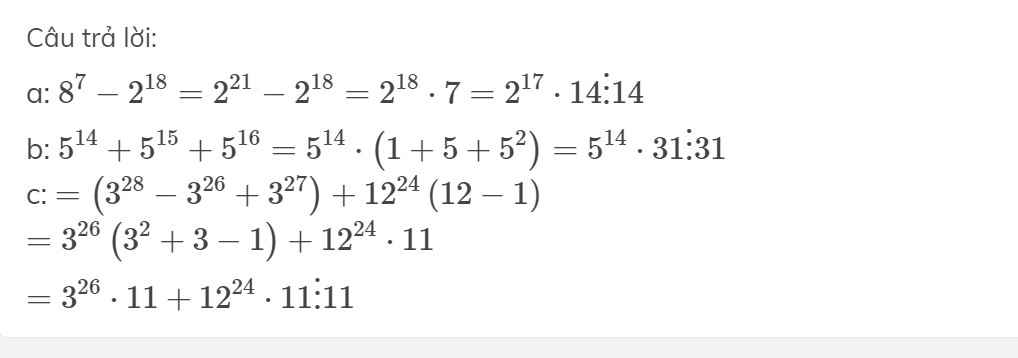chứng tỏ \(5^{14}+5^{15}+5^{16}\) chia hết cho 31
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TA
21 tháng 7 2021
`5^14 + 5^15 + 5^16 = 5^14 . (1+5+5^2) = 5^14 . 31 vdots 31`.
19 tháng 5 2022
a: \(8^7-2^{18}=2^{21}-2^{18}=2^{18}\cdot7=2^{17}\cdot14⋮14\)
b: \(5^{14}+5^{15}+5^{16}=5^{14}\cdot\left(1+5+5^2\right)=5^{14}\cdot31⋮31\)
c: \(=\left(3^{28}-3^{26}+3^{27}\right)+12^{24}\left(12-1\right)\)
\(=3^{26}\left(3^2+3-1\right)+12^{24}\cdot11\)
\(=3^{26}\cdot11+12^{24}\cdot11⋮11\)
4 tháng 7 2017
ta có
\(8^7-2^{18}=8^7-\left(2^3\right)^6\\ =8^7-8^6=8^6\left(8-1\right)\\ =8^6.7=8^5.8.7=8^5.\left(4.2\right).7=14.\left(4.8^5\right)\)
do 14 chia hết cho 14 nên \(14.\left(4.8^5\right)\)cũng chia hết cho 14
hay\(8^7-2^{18}\)chia hết cho 14
các câu b,c bạn làm tương tự. mình chỉ làm cho bạn câu a. chúc bạn học tốt. nếu có vấn đề j về bài toán câu a thì bạn cứ ib cho mình mình sẽ giải đáp.
30 tháng 8 2018
1) nhìn là bt liền : \(2^{16}< 3^{25}\)
2) a) ta có : \(7^{15}-7^{14}+7^{13}=7^{13}\left(7^2-7+1\right)⋮7\left(đpcm\right)\)
b) câu này không CM đc . bn bấm máy nha :)
L
0
NV
1
24 tháng 10 2019
a) Ta có: T= (2+22+23+24)+(25+26+27+28)+.....+(257+258+259+260)
= 30.1 + 25. (2+22+23+24) +.....+ 257. (2+22+23+24)
= 30.1 + 25 . 30 +......+ 257 . 30
=30 . ( 25+...+257)
Vì 30 chia hết cho 30
=> T chia hết cho 30
mà 30 chia hết cho 5
=> T chia hết cho 5
các bài còn lại câu a tương tự bạn tự làm nhé
Phương pháp: nhóm các số hạng để đc 1 số chia hết cho số đó
b) Ta có: S = 165+215
= 220 + 215
=215 . ( 25 + 1)
=215 . 33
Vì 33 chia hết cho 33
=> S chia hết cho 33
CHÚC BẠN HOK TỐT!!!!!!