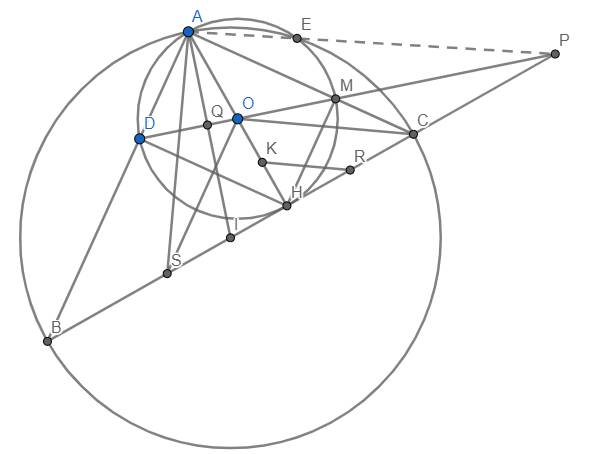
Cho đường tròn tâm O, đường kính BC. A thuộc đường tròn tâm O. AH vuông góc BC. Đường tròn đường kính AH cắt AB, AC và cắt đường tròn tâm O tại E, F, K.
a) Chứng minh: AO vuông góc EF.
b) AK cắt BC tại T. Chứng minh: T, E, F thẳng hàng.
Mọi người giúp em với ạ em cần gấp


a) Vì AH là đường kính \(\Rightarrow\angle AEH=\angle AFH=90\)
Vì BC là đường kính \(\Rightarrow\angle BAC=90\Rightarrow\angle AEH=\angle AFH=\angle EAF=90\)
\(\Rightarrow AEHF\) là hình chữ nhật
\(\Rightarrow\angle AEF=\angle AHF=\angle ACH\left(=90-\angle HAC\right)\)
\(\Rightarrow\angle AEF+\angle ABC=\angle ACH+\angle ABC=90\)
mà \(\angle ABC=\angle BAO\) (\(\Delta ABO\) cân tại O)
\(\Rightarrow\angle AEF+\angle BAO=90\Rightarrow EF\bot AO\)
c) EF cắt BC tại T'.T'A cắt (O) tại K'
Vì \(\angle AEF=\angle ACH\Rightarrow EFCB\) nội tiếp
Xét \(\Delta T'EB\) và \(\Delta T'CF:\) Ta có: \(\left\{{}\begin{matrix}\angle T'EB=\angle T'CF\\\angle FT'Cchung\end{matrix}\right.\)
\(\Rightarrow\Delta T'EB\sim\Delta T'CF\left(g-g\right)\Rightarrow\dfrac{T'E}{T'C}=\dfrac{T'B}{T'F}\Rightarrow T'E.T'F=T'B.T'C\)
Vì AK'BC nội tiếp \(\Rightarrow\angle T'K'B=\angle T'CA\)
Xét \(\Delta T'K'B\) và \(\Delta T'CA:\) Ta có: \(\left\{{}\begin{matrix}\angle T'K'B=\angle T'CA\\\angle AT'Cchung\end{matrix}\right.\)
\(\Rightarrow\Delta T'K'B\sim\Delta T'CA\left(g-g\right)\Rightarrow\dfrac{T'K'}{T'C}=\dfrac{T'B}{T'A}\Rightarrow T'K'.T'A=T'B.T'C\)
\(\Rightarrow T'K'.T'A=T'E.T'F\Rightarrow\dfrac{T'K'}{T'F}=\dfrac{T'E}{T'A}\)
Xét \(\Delta T'EK'\) và \(\Delta T'AF:\) Ta có: \(\left\{{}\begin{matrix}\dfrac{T'K'}{T'F}=\dfrac{T'E}{T'A}\\\angle FT'Achung\end{matrix}\right.\)
\(\Rightarrow\Delta T'EK'\sim\Delta T'AF\left(c-g-c\right)\Rightarrow\angle T'K'E=\angle T'FA\)
\(\Rightarrow AK'EF\) nội tiếp \(\Rightarrow K'\in\) đường tròn đường kính AH
\(\Rightarrow K'\equiv K\Rightarrow T'\equiv T\Rightarrow T,E,F\) thẳng hàng