Giúp mình bài 14 15 với
Giải chi tiết dễ hiểu hộ mk nha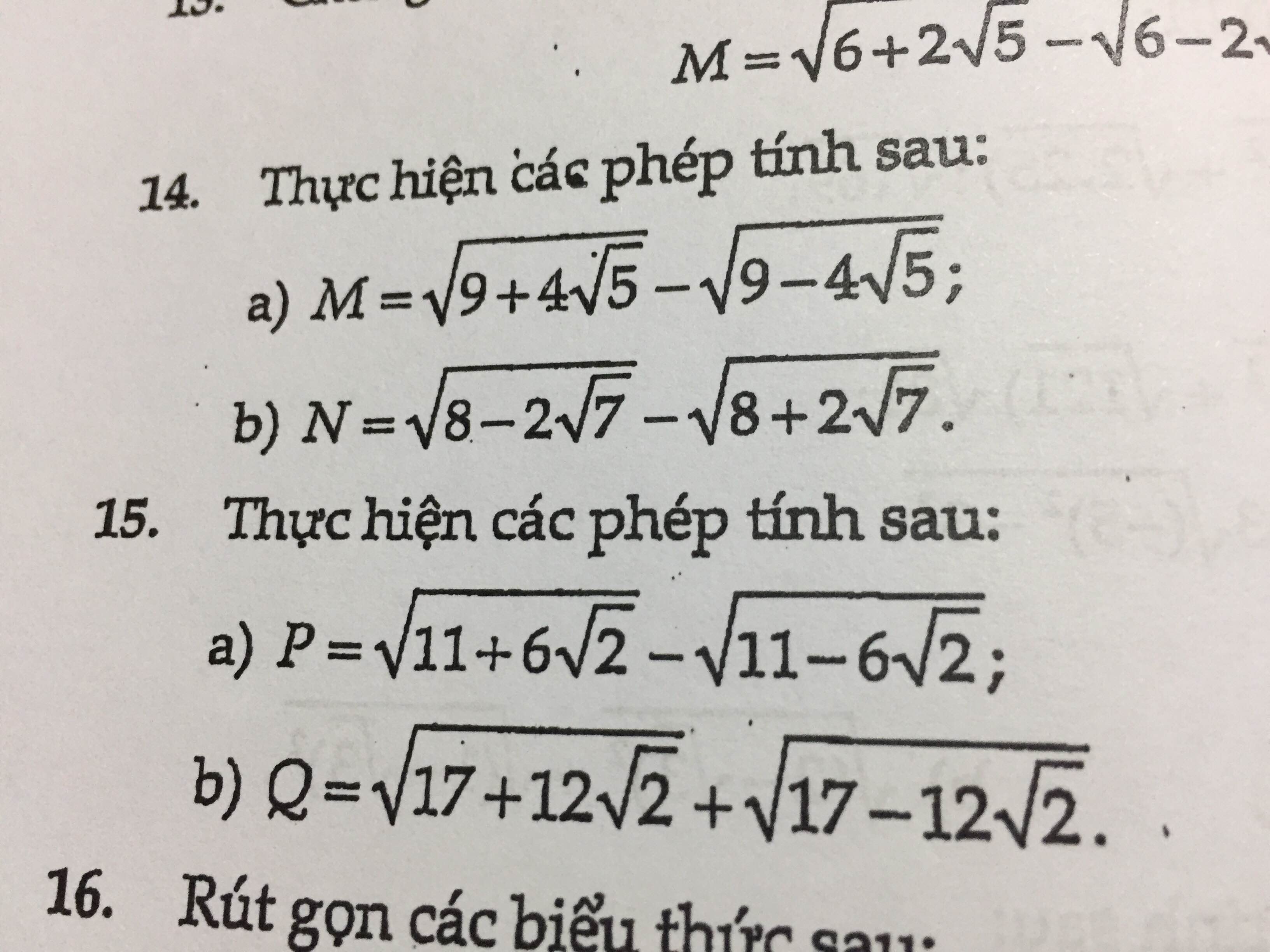
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(CuO+CO\underrightarrow{t^o}Cu+CO_2\)
\(MgO+CO->\left(CO.ko.khử,đc\right)\)
\(Fe_2O_3+3CO\underrightarrow{t^o}2Fe+3CO_2\)
\(FeO+CO\underrightarrow{t^o}Fe+CO_2\)
\(n_{CO_2}=\dfrac{4,48}{22,4}=0,2\left(mol\right)\)
Từ các pthh trên thấy: \(n_{CO_2.sinh.ra}=n_{CO.pứ}=0,2\left(mol\right)\left(theo.tỉ.lệ.pthh\right)\)
Áp dụng ĐLBTKL có: \(m_{hh}+m_{CO}=m_{rắn}+mCO_2\)
=> \(m_{rắn}=m_{hh}+m_{CO}-m_{CO_2}=12,5+0,2.28-0,2.44=9,3\left(g\right)\)

- Gọi quãng đường AB là x (km)
vì thời gian là bằng quãng đường chia vận tốc, ta có:
- Thời gian của ô tô là \(\dfrac{x}{50}\) (km)
- Thời gian của xe máy là \(\dfrac{x}{40}\) (km)
vì ta dùng đơn vị là km/h nên ta phải đổi 30 phút qua giờ, ta có:
- Đổi: 30 phút = 0,5 giờ
vì thời gian đi của ô tô ít hơn xe máy là 0,5 giờ nên ta có phương trình:
\(\dfrac{x}{40}\) \(-\) \(\dfrac{x}{50}\) = 0,5
\(\Leftrightarrow\) \(\dfrac{x\times50}{40\times50}\)\(-\)\(\dfrac{x\times40}{50\times40}\) = \(\dfrac{0,5\times40\times50}{40\times50}\)
\(\Leftrightarrow\) \(\dfrac{50x}{40\times50}\)\(-\dfrac{40x}{50\times40}=\dfrac{1000}{50\times40}\)
\(\Rightarrow\) 50x - 40x = 1000
\(\Leftrightarrow\)10x = 1000
\(\Leftrightarrow\) x = 1000 : 10
\(\Leftrightarrow\) x = 100
vậy quãng đường AB là 100 (km)
----chúc cậu học tốt----
Đổi \(30phút=\dfrac{1}{2}h\)
Gọi quãng đường AB là \(x\left(km;x>0\right)\)
Thì thời gian ô tô đi từ A đến B là \(\dfrac{x}{50}\left(h\right)\)
Thời gian xe máy đi từ A đến B là \(\dfrac{x}{40}\left(h\right)\)
Vì thời gian đi từ A đến B của ô tô ít hơn của xe máy là \(\dfrac{1}{2}h\) nên ta có phương trình :
\(\dfrac{x}{40}-\dfrac{x}{50}=\dfrac{1}{2}\)
\(\Leftrightarrow5x-4x=100\)
\(\Leftrightarrow x=100\left(nhận\right)\)
Vậy quãng đường AB dài \(100km\)

\(n_{NO}=\dfrac{2,24}{22,4}=0,1\left(mol\right)\)
\(3R+8HNO_3\rightarrow3R\left(NO_3\right)_2+2NO+4H_2O\)
từ pthh suy ra: \(n_R=\dfrac{3}{2}.n_{NO}=\dfrac{3}{2}.0,1=0,15\left(mol\right)\)
=> \(M_R=\dfrac{9,75}{0,15}=65\)
Vậy tên của R: kẽm (Zn)


(14,78-a)/(2,87+a)=4/1
14,78+2,87=17,65
Tổng số phần bằng nhau là 4+1=5
Mỗi phần có giá trị bằng 17,65/5=3,53
=>2,87+a=3,53
=>a=0,66.

Dễ thấy với a,b >0 thì (a+b)/2 ≥ √ab <=> 1/(a+b) ≤ 1/4 (1/a +1/b)
Áp dụng bất đẳng thức Cauchy ta được
1/(a+2b+3c)=1/[(a+c)+2(b+c)]≤ 1/4[1/(a+c)+1/2(b+c)] (lại áp dụng tiếp được)
≤ 1/16a+1/16c+1/32b+1/32c
=1/16a+1/32b+3/32c
Trường hợp này dấu "=" xảy ra <=> a+c=2(b+c);a=c;b=c <=> c= 0 mâu thuẩn giả thiết
Do đó dấu "=" không xảy ra
Thế thì 1/(a+2b+3c)<1/16a+1/32b+3/32c (1)
Tương tự 1/( b+2c+3a)<1/16b+1/32c+3/32a (2)
1/ ( c+2a+3b) < 1/16c+1/32a+3/32b (3)
Cộng (1)(2)(3) cho ta
1/( a+2b+3c) + 1/( b+2c+3a) + 1/ ( c+2a+3b) <(1/16+1/32+3/32)(1/a+1/b+1/c)
=3/16*(ab+bc+ca)abc= 3/16
tk nha mk trả lời đầu tiên đó!!!
 giúp mk với, mk cần gấp ạ. camon mn rất nhìu, giải chi tiết dễ hiểu giúp mk nha
giúp mk với, mk cần gấp ạ. camon mn rất nhìu, giải chi tiết dễ hiểu giúp mk nha



14a) \(M=\sqrt{9+4\sqrt{5}}-\sqrt{9-4\sqrt{5}}\)
\(=\sqrt{\left(\sqrt{5}\right)^2+2.\sqrt{2}.2+2^2}-\sqrt{\left(\sqrt{5}\right)^2-2.\sqrt{2}.2+2^2}\)
\(=\sqrt{\left(\sqrt{5}+2\right)^2}-\sqrt{\left(\sqrt{5}-2\right)^2}=\left|\sqrt{5}+2\right|-\left|\sqrt{5}-2\right|\)
\(=\sqrt{5}+2-\sqrt{5}+2=4\)
b) \(N=\sqrt{8-2\sqrt{7}}-\sqrt{8+2\sqrt{7}}\)
\(=\sqrt{\left(\sqrt{7}\right)^2-2.\sqrt{7}.1+1^2}-\sqrt{\left(\sqrt{7}\right)^2+2.\sqrt{7}.1+1^2}\)
\(=\sqrt{\left(\sqrt{7}-1\right)^2}-\sqrt{\left(\sqrt{7}+1\right)^2}=\left|\sqrt{7}-1\right|-\left|\sqrt{7}+1\right|\)
\(=\sqrt{7}-1-\sqrt{7}-1=-2\)
15a) \(P=\sqrt{11+6\sqrt{2}}-\sqrt{11-6\sqrt{2}}\)
\(=\sqrt{3^2+2.3.\sqrt{2}+\left(\sqrt{2}\right)^2}-\sqrt{3^2-2.3.\sqrt{2}+\left(\sqrt{2}\right)^2}\)
\(=\sqrt{\left(3+\sqrt{2}\right)^2}-\sqrt{\left(3-\sqrt{2}\right)^2}=\left|3+\sqrt{2}\right|-\left|3-\sqrt{2}\right|\)
\(=3+\sqrt{2}-3+\sqrt{2}=2\sqrt{2}\)
b) \(Q=\sqrt{17+12\sqrt{2}}+\sqrt{17-12\sqrt{2}}\)
\(=\sqrt{3^2+2.3.2\sqrt{2}+\left(2\sqrt{2}\right)^2}+\sqrt{3^2-2.3.2\sqrt{2}+\left(2\sqrt{2}\right)^2}\)
\(=\sqrt{\left(3+2\sqrt{2}\right)^2}+\sqrt{\left(3-2\sqrt{2}\right)^2}=\left|3+2\sqrt{2}\right|+\left|3-2\sqrt{2}\right|\)
\(=3+2\sqrt{2}+3-2\sqrt{2}=6\)