Với những giá trị nguyên nào của x thì phân số sau tối giản:
a, \(\dfrac{x-8}{2x-17}\)
b, \(\dfrac{x-4}{x+1}\)
Cảm ơn bạn!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
BN
0
NH
0
L
8 tháng 8 2019
a)\(\frac{x-8}{2x-17}\)
Gọi d thuộc ƯC(x-8,2x-17)
=>x-8 chia hết cho d=>2(x-8) chia hết cho d=>2x-16 chia hết cho d
=>2x-17 chia hết cho d
=>(2x-16)-(2x-17) chia hết cho d
=>2x-16-2x+17 chia hết cho d
=>1 chia hết cho d
=> d thuộc Ư(1)=\([1;1]\)
=>Phân số trên tối giản vs mọi giá trị của x
Học tốt
13 tháng 3 2022
a, \(x-1\inƯ\left(-3\right)=\left\{\pm1;\pm3\right\}\)
| x-1 | 1 | -1 | 3 | -3 |
| x | 2 | 0 | 4 | -2 |
b, \(2x-1\inƯ\left(-4\right)=\left\{\pm1;\pm2;\pm4\right\}\)
| 2x-1 | 1 | -1 | 2 | -2 | 4 | -4 |
| x | 1 | 0 | loại | loại | loại | loại |
c, \(\dfrac{3\left(x-1\right)+10}{x-1}=3+\dfrac{10}{x-1}\Rightarrow x-1\inƯ\left(10\right)=\left\{\pm1;\pm2;\pm5;\pm10\right\}\)
| x-1 | 1 | -1 | 2 | -2 | 5 | -5 | 10 | -10 |
| x | 2 | 0 | 3 | -1 | 6 | -4 | 11 | -9 |
d, \(\dfrac{4\left(x-3\right)+3}{-\left(x-3\right)}=-4-\dfrac{3}{x+3}\Rightarrow x+3\inƯ\left(-3\right)=\left\{\pm1;\pm3\right\}\)
| x+3 | 1 | -1 | 3 | -3 |
| x | -2 | -4 | 0 | -6 |
TT
15 tháng 1 2021
x đầu ở đa thức A là x^3 chăng?
a/ \(A=x^3-5x^2+8x-4\)
\(=\left(x^3-x^2\right)+\left(-4x^2+4\right)+\left(8x-8\right)\)
\(=x^2\left(x-1\right)-4\left(x-1\right)\left(x+1\right)+8\)
\(=\left(x-1\right)\left(x^2-4x-4\right)=\left(x-1\right)\left(x-2\right)^2\)
b/ \(B=\dfrac{x^5}{30}-\dfrac{x^3}{6}+\dfrac{2x}{15}\)
\(=\dfrac{x^5}{30}-\dfrac{5x^3}{30}+\dfrac{4x}{30}\)
\(=\dfrac{x\left(x^4-5x^2+4\right)}{30}\)
\(=\dfrac{x\left(x^4-x^2-4x^2+4\right)}{30}\)
\(=\dfrac{x\left(x+2\right)\left(x-1\right)\left(x+1\right)\left(x-2\right)}{30}\)
UK
0
27 tháng 6 2019
Để phân số đó tối giản ta cần chứng minh tử và mẫu là 2 số nguyên tố cùng nhau
Đặt ( x-8; 2x-17)=d (d khác 0)
x-8 chia hết cho d
2(x-8) chia hết cho d hay 2x-16 chia hết cho d
Mặt khác 2x-17 chia hết cho d=> (2x-16)(2x-17) chia hết cho d
<=> 1 chia hết cho d => d=1
=> x-8 và 2x-17 là 2 số nguyên tố cùng nhau
=> Phân số đó tối giản với mọi giá trị của x
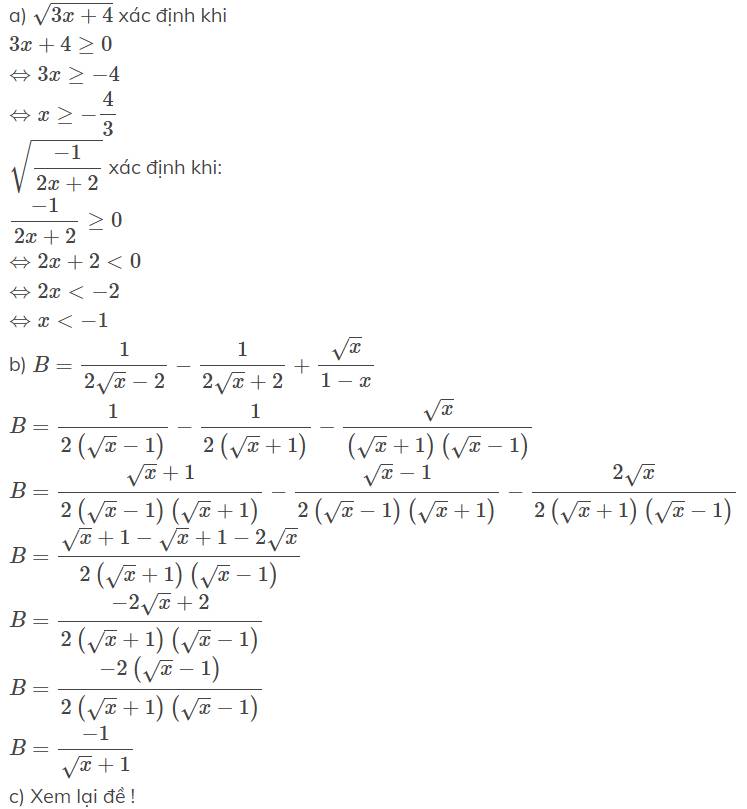
a.x=9
b.x=5
phải giải từng bước ra chứ bạn!!!