Cho dây MN là đường trung trực của bán kính OH của đường tròn (O; R). Gọi P , Q lần lượt là giao điểm của OM và ON với tiếp tuyến tại H của đường tròn (O). Tính PQ theo R
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho đường tròn (O), bán kính OA, dây CD là đường trung trực của OA. Tứ giác OCAD là hình gì? Vì sao?

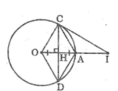
Gọi H là giao điểm của OA và CD
Vì CD là đường trung trực của OA nên:
CD ⊥ OA và HA = HO
Mà CD ⊥ OA nên HC = HD (đường kính dây cung)
Vì tứ giác ACOD có hai đường chéo cắt nhau tại trung điểm mỗi đường nên nó là hình bình hành.
Dồng thời CD ⊥ OA nên ACOD là hình thoi

a: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó:ΔACB vuông tại C
=>\(\widehat{ACB}=90^0\)
Ta có: ΔOAC cân tại O(OA=OC)
mà OH là đường trung tuyến
nên OH\(\perp\)AC và OH là tia phân giác của góc AOC
Ta có: OH\(\perp\)AC(cmt)
AC\(\perp\)CB tại C(Do ΔACB vuông tại C)
Do đó: OH//BC
b:
OH là phân giác của góc AOC
=>\(\widehat{AOH}=\widehat{COH}\)
mà M\(\in\)OH
nên \(\widehat{AOM}=\widehat{COM}\)
Xét ΔOCM và ΔOAM có
OC=OA
\(\widehat{COM}=\widehat{AOM}\)
OM chung
Do đó: ΔOCM=ΔOAM
=>\(\widehat{OCM}=\widehat{OAM}\)
mà \(\widehat{OCM}=90^0\)
nên \(\widehat{OAM}=90^0\)
=>OA\(\perp\)MA tại A
=>MA là tiếp tuyến tại A của (O)

a: ΔOAB cân tại O
mà OI là đường trung tuyến
nên OI vuông góc AB
I là trung điểm của AB
=>IA=IB=16/2=8cm
ΔOIA vuông tại I
=>OA^2=OI^2+IA^2
=>OI^2=10^2-8^2=36
=>OI=6(cm)
b: OM=OI+IM
=>6+IM=10
=>IM=4cm
ΔMIA vuông tại I
=>MI^2+IA^2=MA^2
=>\(MA=\sqrt{4^2+8^2}=4\sqrt{5}\left(cm\right)\)

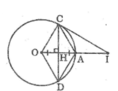
Vì ACOD là hình thoi nên AC = OC
Mà OC = OA (= R) nên tam giác OAC đều


Lời giải:
Tam giác $OAB$ cân tại $O$ (do $OA=OB=R$) nên đường trung tuyến $OH$ đồng thời là đường cao.
$\Rightarrow OH\perp AB$
$AH=\frac{1}{2}AB=8$ (cm)
Áp dụng định lý Pitago cho tam giác vuông $HAO$:
$R=AO=\sqrt{OH^2+AH^2}=\sqrt{6^2+8^2}=10$ (cm)
Đáp án D.

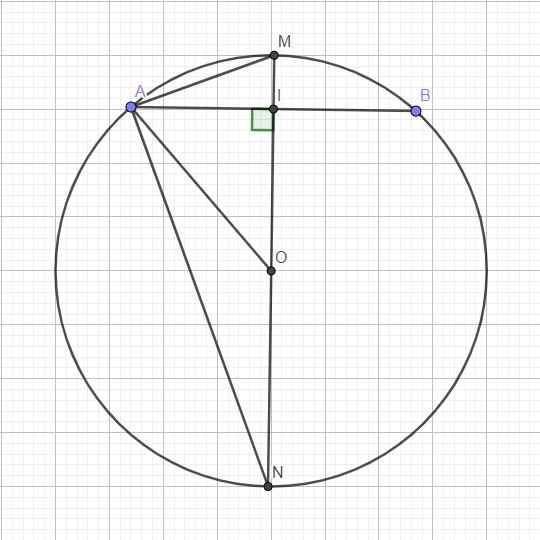
Do I là trung điểm AB \(\Rightarrow OI\perp AB\)
\(AI=\dfrac{1}{2}AB=3\)
Trong tam giác vuông OAI, áp dụng Pitago:
\(OI=\sqrt{OA^2-AI^2}=\sqrt{R^2-AI^2}=4\)
\(\Rightarrow IM=OM-OI=R-OI=1\)
\(\Rightarrow AM=\sqrt{AI^2+IM^2}=\sqrt{10}\left(cm\right)\)
b.
Vẫn như trên, ta có: \(AI=\dfrac{1}{2}AB=6\)
Do MN là đường kính \(\Rightarrow\Delta MAN\) vuông tại A
Áp dụng hệ thức lượng trong tam giác vuông MAN với đường cao AI:
\(\dfrac{1}{AI^2}=\dfrac{1}{AN^2}+\dfrac{1}{AM^2}\Rightarrow\dfrac{1}{6^2}=\dfrac{1}{10^2}+\dfrac{1}{AM^2}\Rightarrow AM=\dfrac{15}{2}\)
Áp dụng hệ thức lượng:
\(AI.MN=AN.AM\Leftrightarrow MN=\dfrac{AM.AN}{AI}=\dfrac{25}{2}\)
\(\Rightarrow R=\dfrac{MN}{2}=\dfrac{25}{4}\left(cm\right)\)
MN cắt OH tại A.
Vì MN là trung trực \(\Rightarrow MN\bot OH\) và A là trung điểm OH
mà \(PQ\bot OH\) \(\Rightarrow PQ\parallel MN\)
Xét \(\Delta OHQ\) có A là trung điểm OH và \(AN\parallel HQ\)
\(\Rightarrow N\) là trung điểm OQ
Tương tự \(\Rightarrow M\) là trung điểm OP
\(\Rightarrow MN\) là đường trung bình tam giác OPQ
\(\Rightarrow PQ=2MN\)
Vì MN là trung trực OH \(\Rightarrow MH=MO=OH\left(=R\right)\Rightarrow\Delta MOH\) đều
\(\Rightarrow MA=sinMHA.MH=sin60.R=\dfrac{\sqrt{3}}{2}R\Rightarrow MN=\sqrt{3}R\)
\(\Rightarrow PQ=2\sqrt{3}R\)
mình cảm ơn