Giúp mình bài trong hình với , làm đủ + chi tiết hộ mình
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Em chia nhỏ bài ra mỗi bài đăng 1 lượt hỏi nha!
Bài 6:
a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó: ΔABD=ΔACE
b: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
=>AM⊥DE

14a) \(M=\sqrt{9+4\sqrt{5}}-\sqrt{9-4\sqrt{5}}\)
\(=\sqrt{\left(\sqrt{5}\right)^2+2.\sqrt{2}.2+2^2}-\sqrt{\left(\sqrt{5}\right)^2-2.\sqrt{2}.2+2^2}\)
\(=\sqrt{\left(\sqrt{5}+2\right)^2}-\sqrt{\left(\sqrt{5}-2\right)^2}=\left|\sqrt{5}+2\right|-\left|\sqrt{5}-2\right|\)
\(=\sqrt{5}+2-\sqrt{5}+2=4\)
b) \(N=\sqrt{8-2\sqrt{7}}-\sqrt{8+2\sqrt{7}}\)
\(=\sqrt{\left(\sqrt{7}\right)^2-2.\sqrt{7}.1+1^2}-\sqrt{\left(\sqrt{7}\right)^2+2.\sqrt{7}.1+1^2}\)
\(=\sqrt{\left(\sqrt{7}-1\right)^2}-\sqrt{\left(\sqrt{7}+1\right)^2}=\left|\sqrt{7}-1\right|-\left|\sqrt{7}+1\right|\)
\(=\sqrt{7}-1-\sqrt{7}-1=-2\)
15a) \(P=\sqrt{11+6\sqrt{2}}-\sqrt{11-6\sqrt{2}}\)
\(=\sqrt{3^2+2.3.\sqrt{2}+\left(\sqrt{2}\right)^2}-\sqrt{3^2-2.3.\sqrt{2}+\left(\sqrt{2}\right)^2}\)
\(=\sqrt{\left(3+\sqrt{2}\right)^2}-\sqrt{\left(3-\sqrt{2}\right)^2}=\left|3+\sqrt{2}\right|-\left|3-\sqrt{2}\right|\)
\(=3+\sqrt{2}-3+\sqrt{2}=2\sqrt{2}\)
b) \(Q=\sqrt{17+12\sqrt{2}}+\sqrt{17-12\sqrt{2}}\)
\(=\sqrt{3^2+2.3.2\sqrt{2}+\left(2\sqrt{2}\right)^2}+\sqrt{3^2-2.3.2\sqrt{2}+\left(2\sqrt{2}\right)^2}\)
\(=\sqrt{\left(3+2\sqrt{2}\right)^2}+\sqrt{\left(3-2\sqrt{2}\right)^2}=\left|3+2\sqrt{2}\right|+\left|3-2\sqrt{2}\right|\)
\(=3+2\sqrt{2}+3-2\sqrt{2}=6\)

(x + 2)(x + 5) < 0
Th1: x + 2 > 0 => x > -2
x + 5 < 0 => x < -5
=> Vô lý
Th2: x + 2 < 0 => x < -2
x + 5 > 0 => x > -5
=> -5 < x < -2
Ta có : (x+2)(x+5)<0
=> x+2 và x+5 là hai số nguyên trái dấu
mà x+5 > x+2
=> \(\hept{\begin{cases}x+5>0\\x+2< 0\end{cases}}\)
=> \(\hept{\begin{cases}x>-5\\x< 2\end{cases}}\)
=> \(-5< x< 2\)
=> \(x\in\left\{-4;-3;-2;-1;0;1\right\}\)
~ học tốt nha ~

\(M=x^4-4x+7=\left(x^2-4x+4\right)+3=\left(x-2\right)^2+3\ge3\)
\(minM=3\Leftrightarrow x=2\)
\(P=x^2-6x+y^2-2y+12=\left(x^2-6x+9\right)+\left(y^2-2y+1\right)+2=\left(x-3\right)^2+\left(y-1\right)^2+2\ge2\)
\(minP=2\Leftrightarrow\)\(\left\{{}\begin{matrix}x=3\\y=1\end{matrix}\right.\)

a:\(\dfrac{33}{44}=\dfrac{3}{4}\\ MSC:8\\ \dfrac{3}{4}=\dfrac{3\times2}{4\times2}=\dfrac{6}{8};\dfrac{2}{8}\)
b:\(\dfrac{9}{12}=\dfrac{3}{4};\dfrac{24}{36}=\dfrac{7}{9}\\ MSC:72\\ \dfrac{3}{4}=\dfrac{3\times18}{4\times18}=\dfrac{54}{72};\dfrac{7}{9}=\dfrac{7\times8}{9\times8}=\dfrac{56}{72};\dfrac{3}{8}=\dfrac{3\times9}{8\times9}=\dfrac{27}{72}\)

đề như thế này à \(\dfrac{\sqrt{27-3\sqrt{2}+2\sqrt{6}}}{3\sqrt{3}}\)

Bài 2:
a. Áp dụng định lý Pitago:
$BC=\sqrt{AB^2+AC^2}=\sqrt{3^2+4^2}=5$ (cm)
$AH=\frac{2S_{ABC}}{BC}=\frac{AB.AC}{BC}=\frac{3.4}{5}=2,4$ (cm)
Áp dụng định lý Pitago:
$BH=\sqrt{AB^2-AH^2}=\sqrt{3^2-2,4^2}=1,8$ (cm)
$CH=\sqrt{AC^2-AH^2}=\sqrt{4^2-2,4^2}=3,2$ (cm)
b.
Áp dụng hệ thức lượng trong tam giác vuông:
$AH^2=BH.CH=9.16$
$\Rightarrow AH=12$ (cm)
Áp dụng định lý Pitago:
$AB=\sqrt{AH^2+BH^2}=\sqrt{12^2+9^2}=15$ (cm)
$AC=\sqrt{AH^2+CH^2}=\sqrt{12^2+16^2}=20$ (cm)
$BC=BH+CH=9+16=25$ (cm)
Bài 3:
Vì $AB:AC=3:4$ nên đặt $AB=3a; AC=4a$ (cm)
Áp dụng định lý Pitago:
$15=BC=\sqrt{AB^2+AC^2}=\sqrt{(3a)^2+(4a)^2}=5a$
$\Rightarrow a=3$ (cm)
$AH=\frac{AB.AC}{BC}=\frac{3a.4a}{5a}=2,4a$ (cm)
$BH=\sqrt{AB^2-AH^2}=\sqrt{(3a)^2-(2,4a)^2}=1,8a=1,8.3=5,4$ (cm)
$CH=\sqrt{AC^2-AH^2}=\sqrt{(4a)^2-(2,4a)^2}=3,2a=3,2.3=9,6$ (cm)
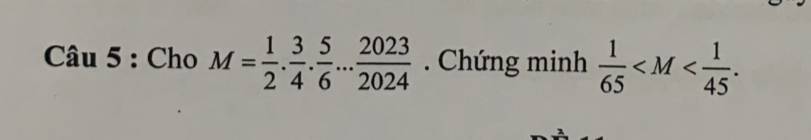

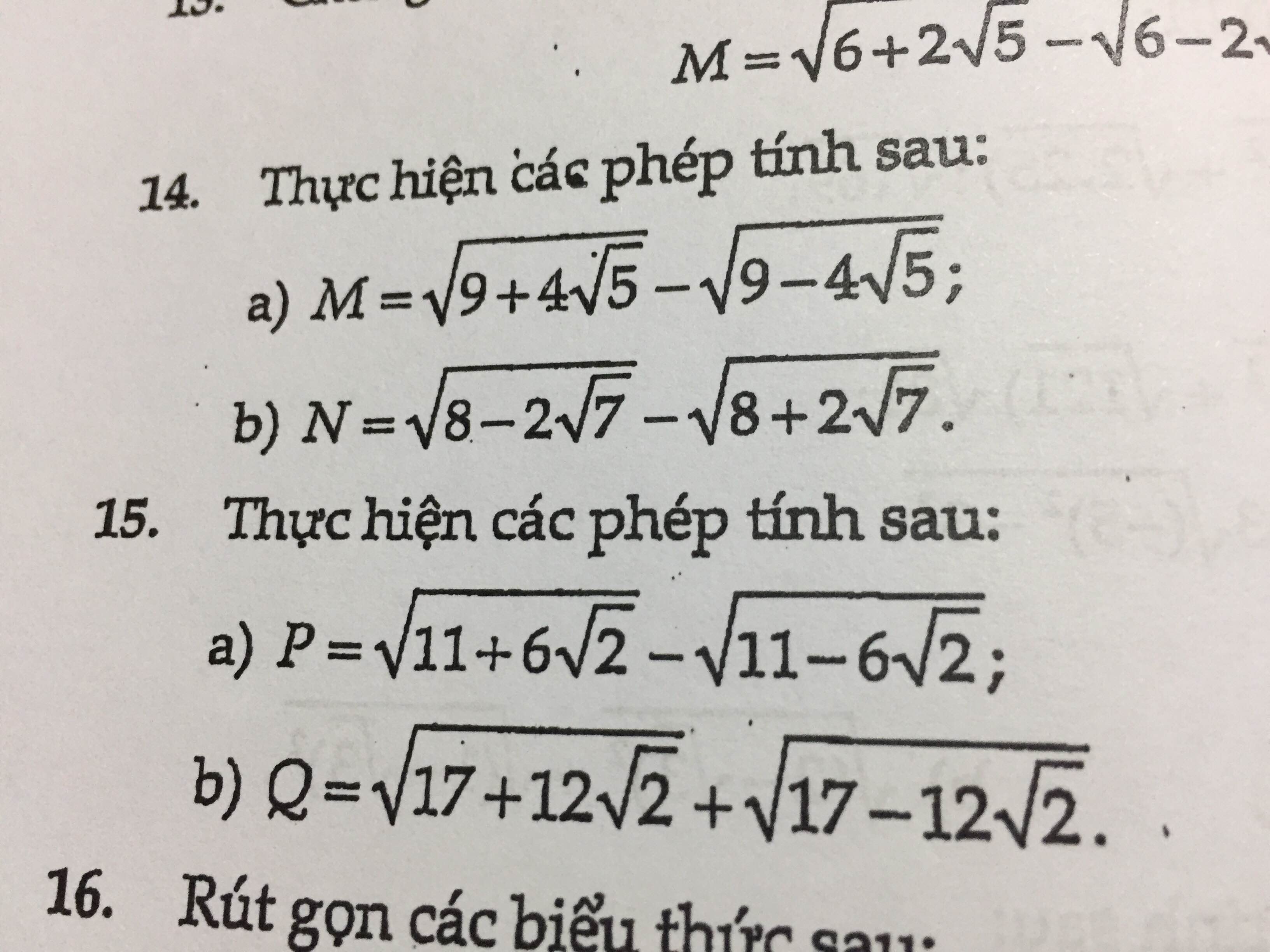
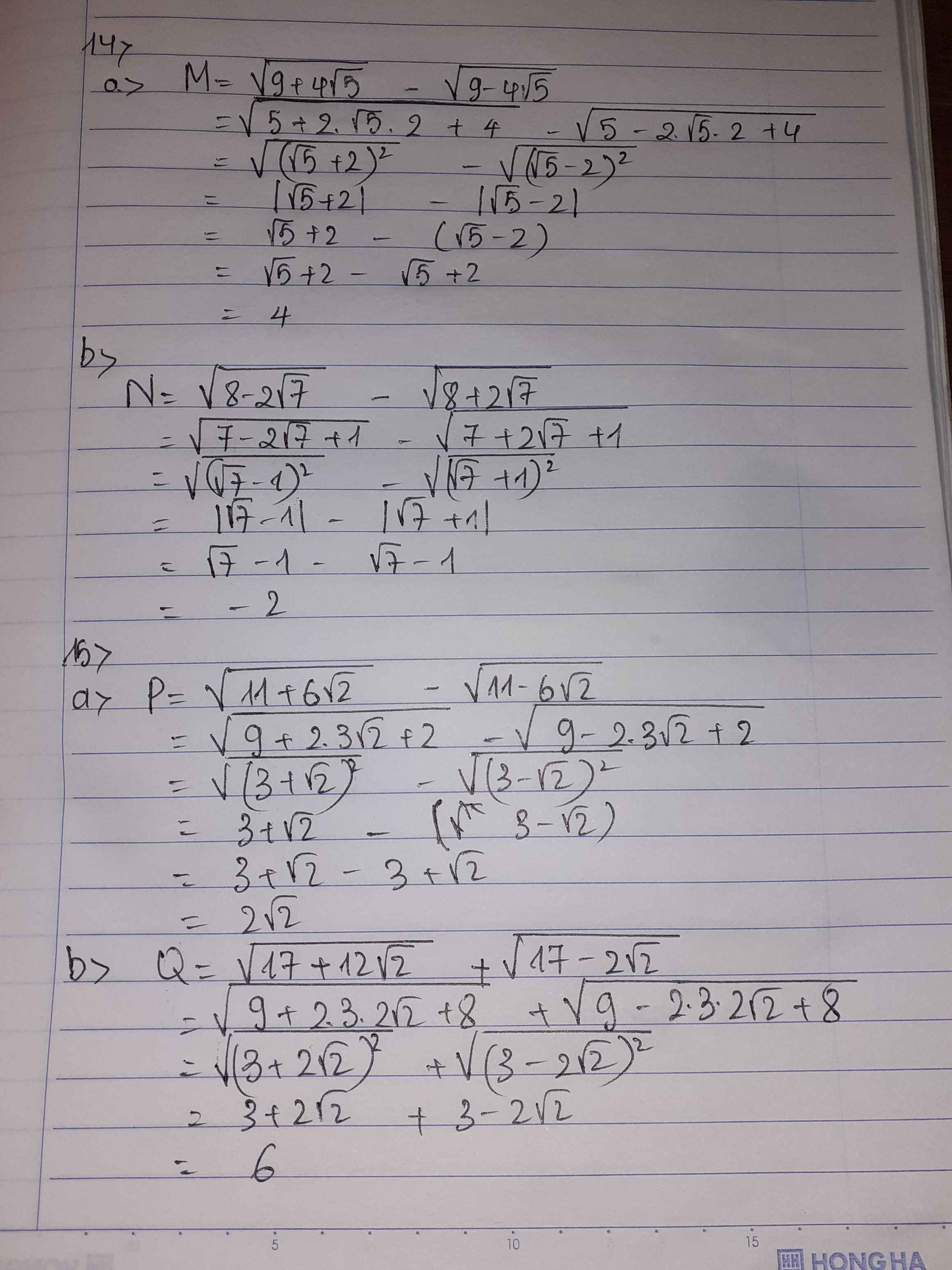

Tham khảo
vi phạm phương châm quan hệ.
vì sử dụng từ đồng âm khác nghĩa làm sai ý ngườ hỏi
a) Họp xong bạn nhớ đi ra cửa trước
- Phương châm hội thoại vi phạm: phương châm về lượng ( nội dung cần truyền đạt chưa cụ thể, rõ ràng )
- Sửa lại:
Họp xong bạn nhớ đi ra cửa trước
⇒ Họp xong bạn nhớ đi ra cửa trước của tòa nhà A tầng 1 nhé