chứng tỏ rằng phân số 1/5 là phân số tối giản
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HT
12 tháng 7 2015
Có cần mik chứng mik \(\frac{2n+1}{n-5}\)không là phân số tối giản không?
PT
1
CM
27 tháng 11 2017
Đặt d = ƯCLN( 14n + 3, 21n + 5 ) ( d ∈ N* )
Ta có: 14n + 3 ⋮ d và 21n + 5 ⋮ d
⇒ 3( 14n + 3 ) ⋮ d và 2( 21n + 5 ) ⋮ d ⇒ 42n + 9 ⋮ d và 42n + 10 ⋮ d
⇒ ( 42n + 9 ) – ( 42n + 10 ) ⋮ d ⇒ 1 ⋮ d . Do đó d = 1
Vậy 14 n + 3 21 n + 5 là phân số tối giản
PT
1
PT
1
CM
18 tháng 12 2019
Đặt d = ƯCLN( 14n + 3, 21n + 5 ) ( d ∈ N* )
Ta có: 14n + 3 ⋮ d và 21n + 5 ⋮ d
⇒ 3( 14n + 3 ) ⋮ d và 2( 21n + 5 ) ⋮ d ⇒ 42n + 9 ⋮ d và 42n + 10 ⋮ d
⇒ ( 42n + 9 ) – ( 42n + 10 ) ⋮ d ⇒ 1 ⋮ d . Do đó d = 1
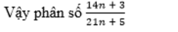là phân số tối giản.
HT
2
1 tháng 4 2016
GỌI Đ LÀ ƯC (2N+1/3N+2)
=>2N+2 CHIA HẾT CHO Đ=>3(2N+3) CHIA HẾT CHO Đ
=>3N+2CHIA HẾT CHO Đ=>2(3N+4) CHIA HẾT CHO DD
=>(6N+3)-(6N+4) CHIA HẾT CHO Đ
=>1 CHIA HẾT CHO Đ
=>Đ=1
=>2N+1/3N+2 LÀ P/S TỐI GIẢN
ND
3
11 tháng 4 2023
gọi d là ƯCLN(2n+1;3n+2).theo bài ra ta có:
2n+1 chia hết cho d=>6n+3 chia hết cho d
3n+2 chia hết cho d=>6n+4 chia hết cho d
=>1 chia hết cho d=>d=1
vậy ...
VN
Võ Ngọc Phương
VIP
11 tháng 4 2023
Gọi d ϵ ƯCLN\(\left(\dfrac{2n+1}{3n+2}\right)\)
Nên 2n+1⁝ d và 3n+2 ⁝ d
⇒ 3(2n+1) ⁝ d và 2(3n+2)
⇒ 6n+3 ⁝ d và 6n+4 ⁝ d
⇒ ( 6n+4 - 6n+3) ⁝ d
⇒ 1⁝ d
⇒ d= 1
Vậy:..
Chúc bạn học tốt
NT
1
LC
20 tháng 8 2015
Gọi ƯC(5n-4,6n-5)=d
Ta có: 5n-4 chia hết cho d=>6.(5n-4)=30n-24 chia hết cho d
6n-5 chia hết cho d=>5,(6n-5)=30n-25 chia hết cho d
=>30n-24-(30n-25) chia hết cho d
=>1 chia hết cho d
=>d=1
=>(5n-4,6n-5)=1
=>Phân số 5n-4/6n-5 là phân số tối giản.
=>ĐPCM
RA
4
30 tháng 4 2019
Gọi d là ƯCLN ( 2n + 1 ; 3n + 2 )( d thuộc N* )
=> 2n + 1 chia hết cho d ; 3n + 2 chia hết cho d
=> 3( 2n + 1 ) chia hết cho d ; 2( 3n + 2 ) chia hết cho d
=> 6n + 3 chia hết cho d ; 6n + 4 chia hết cho d
=> ( 6n + 4 ) - ( 6n + 3 ) chia hết cho d
=> 6n + 4 - 6n - 3 chia hết cho d
=> 1 chia hết cho d
Mà d thuộc N* => d = 1
=> ƯCLN( 2n + 1 ; 3n + 2 ) = 1
Chứng tỏ phân số 2n + 1/3n + 2 tối giản
vì ƯCLN(1, 5)=1 => 1/5 là phân số tối giản, chúc bạn học tốt nha, ủng hộ mk với nha
Vì tử số và mẫu số của 1/5 không cùng chia hết cho một số nào đó lớn hơn 1 nên nó chính là phân số tối giản.
Chúc bạn hok tốt nha!@##