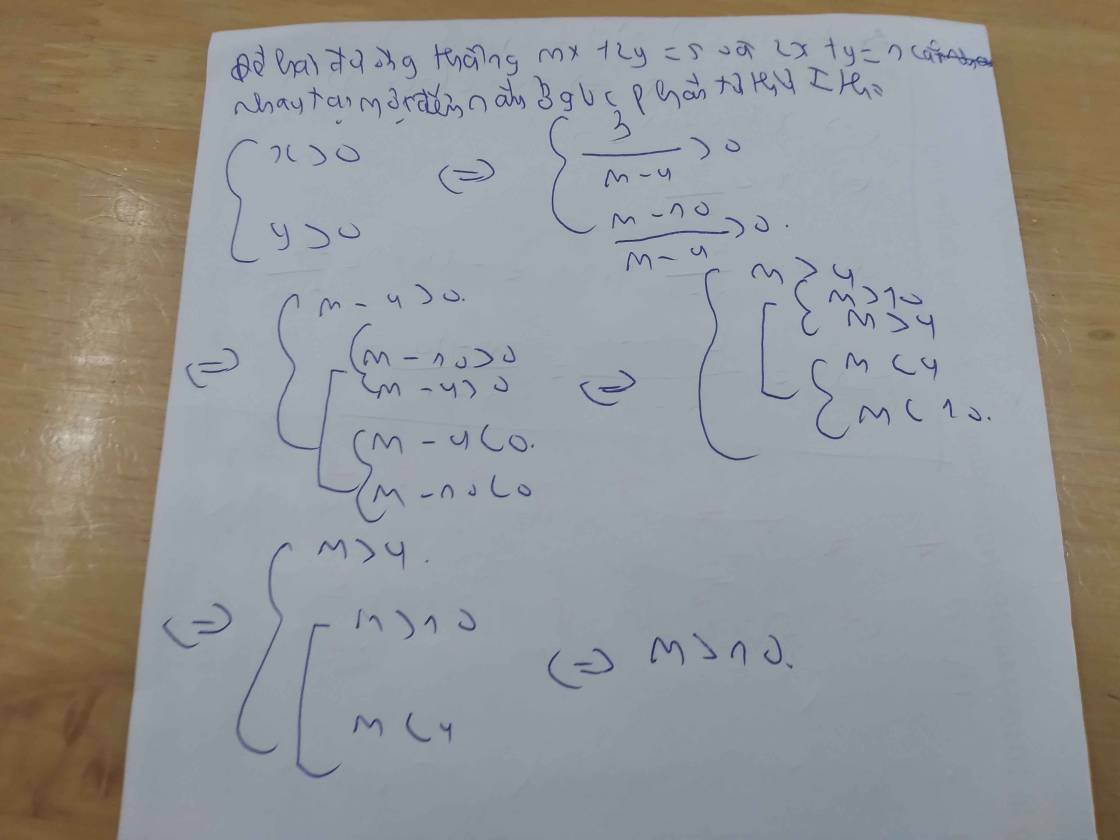
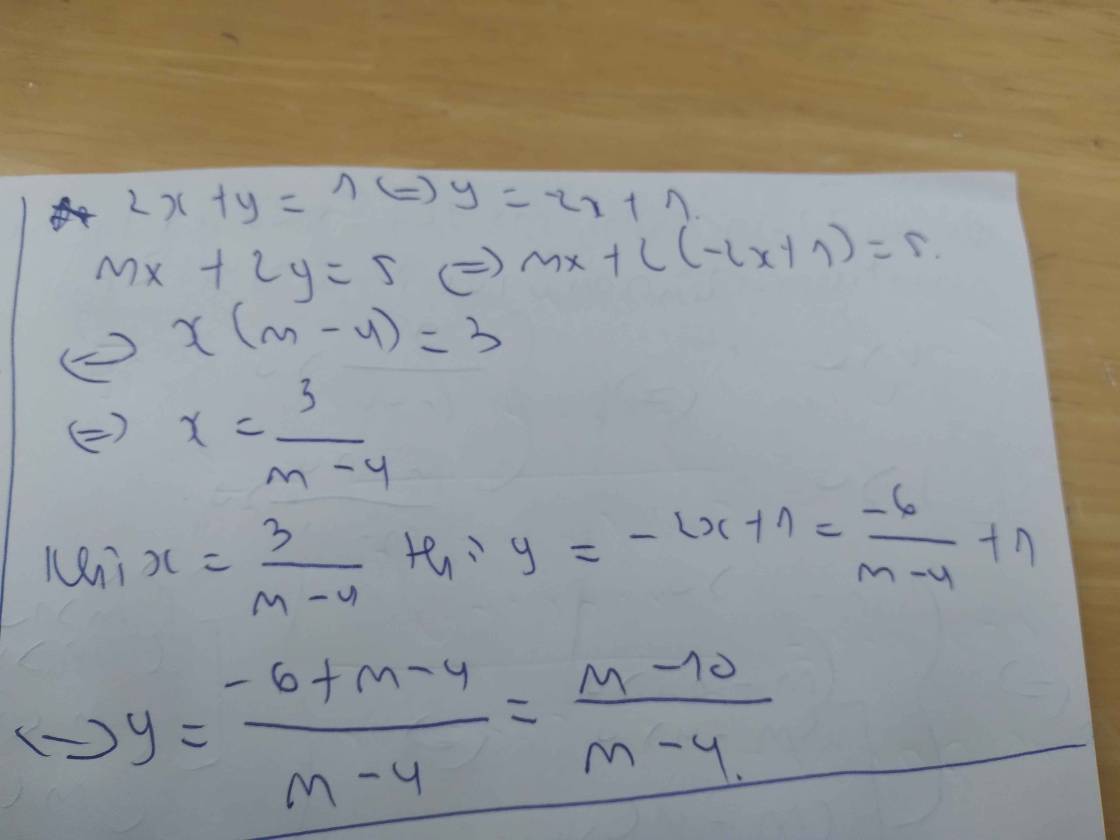Tìm m để đg thẳng y=mx+1 cắt y=2x-1 tại 1 điểm thuộc đg phân giác góc phần tư thứ hai
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left\{{}\begin{matrix}\left(m-1\right)x-my=3m-1\left(1\right)\\2x-y=m+5\left(2\right)\end{matrix}\right.\)
a) Từ (2) => y=2x-m-5, thay vào (1) ta có:
\(\left(m-1\right)x-m\left(2x-m-5\right)=3m-1\)
=>\(\left(m-1\right)x-2mx+m^2=5m-3m+1=0\)
=> \(\left(m-1-2m\right)x+m^2+2m+1=0\)
<=> \(\left(-m-1\right)x+\left(m+1\right)^2=0\)
<=> \(\left(m+1\right)x=\left(m+1\right)^2\) (*)
+Nếu m=-1 => pt (*) tương đương:
0x=0 => pt (*) vô số nghiệm x => y = 2x+1-5 = 2x-4
=> hệ pt có vô số nghiệm (x;2x-4)
+ Nếu m\(\ne\)1 => pt(*) có nghiệm duy nhất x=\(\dfrac{\left(m+1\right)^2}{m+1}=m+1\)
=> y=2.(m+1)-m-5 = 2m+2-m-5=m-3
=> hpt có nghiệm duy nhất (x;y) =(m+1;m-3)
Vậy với m=-1, hệ pt có vô số nghiệm (x;2x-4)
Với m\(\ne\)-1 hệ pt có nghiệm duy nhất (x;y)=(m+1;m-3)
b) Để 2 đường thẳng của hệ cắt nhau tại 1 điểm nằm trong góc phần tư thức IV của hệ tọa độ Oxy thì hệ pt có nghiệm duy nhất x>0, y<0
=> \(\left\{{}\begin{matrix}m+1>0\\m-3< 0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}m>-1\\m< 3\end{matrix}\right.\)
Mà m\(\in\)Z => m\(\in\){0;1;2}
c) Với m≠ -1 thì hệ có nghiệm duy nhất (x;y) = (m+1;m-3)
P=\(x^2+y^2=\left(m+1\right)^2+\left(m-3\right)^2\)
P=\(m^2+2m+1+m^1-6m+9\)
\(P=2m^2-4m+10=2\left(m^2-2m+5\right)=2\left(m^2-2m+1\right)+8=2\left(m-1\right)^2+8\)
Vì (m-1)2 \(\ge\)0 với mọi m ≠-1
=> \(2\left(m-1\right)^2\ge0\)<=> \(2\left(m-1\right)^2+8\ge8\)
=> P\(\ge\) 8
=> P đạt giá trị nhỏ nhất =8 khi m-1=0 <=> m=1

Phương trình hoành độ giao điểm là:
\(\left(m-1\right)x+2m+3=2x+1\)
=>\(\left(m-1\right)x-2x=1-2m-3\)
=>\(x\left(m-3\right)=-2m-2\)
=>\(x=\dfrac{-2m-2}{m-3}\)
\(y=2x+1=\dfrac{2\cdot\left(-2m-2\right)}{m-3}+1=\dfrac{-4m-4+m-3}{m-3}=\dfrac{-3m-7}{m-3}\)
Để (d) cắt đường thẳng y=2x+1 tại một điểm thuộc góc phần tư thứ nhất thì
\(\left\{{}\begin{matrix}m-1\ne2\\\dfrac{-2m-2}{m-3}< 0\\\dfrac{-3m-7}{m-3}>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m\ne2\left(5\right)\\\dfrac{m+1}{m-3}>0\left(1\right)\\\dfrac{3m+7}{m-3}< 0\left(2\right)\end{matrix}\right.\)
(1); \(\dfrac{m+1}{m-3}>0\)
TH1: \(\left\{{}\begin{matrix}m+1>0\\m-3>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m>-1\\m>3\end{matrix}\right.\)
=>m>3
TH2: \(\left\{{}\begin{matrix}m+1< 0\\m-3< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m< -1\\m< 3\end{matrix}\right.\)
=>m<-1
Vậy: \(m\in\left(3;+\infty\right)\cup\left(-\infty;-1\right)\)(3)
(2): \(\dfrac{3m+7}{m-3}< 0\)
TH1: \(\left\{{}\begin{matrix}3m+7>0\\m-3< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m>-\dfrac{7}{3}\\m< 3\end{matrix}\right.\)
=>\(\dfrac{-7}{3}< m< 3\)
TH2: \(\left\{{}\begin{matrix}3m+7< 0\\m-3>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m>3\\m< -\dfrac{7}{3}\end{matrix}\right.\)
=>Loại
Vậy: \(-\dfrac{7}{3}< m< 3\)(4)
Từ (3),(4),(5) suy ra \(\left\{{}\begin{matrix}m\ne2\\-\dfrac{7}{3}< m< 3\\m\in\left(3;+\infty\right)\cup\left(-\infty;-1\right)\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m\ne2\\m\in\left(-\dfrac{7}{3};-1\right)\end{matrix}\right.\)
=>\(m\in\left(-\dfrac{7}{3};-1\right)\)

Phương trình hoành độ giao điểm là:
\(\dfrac{1}{2}x^2-3mx+2=0\)
\(\text{Δ}=\left(-3m\right)^2-4\cdot\dfrac{1}{2}\cdot2=9m^2-4\)
Để phương trình có hai nghiệm phân biệt thì Δ>0
\(\Leftrightarrow\left[{}\begin{matrix}m>\dfrac{2}{3}\\m< -\dfrac{2}{3}\end{matrix}\right.\)

a, Đường phân giác góc phần tư thứ nhất là một nửa đường thẳng x - y = 0 nằm ở góc phần tư thứ nhất
=> d nhận (1 ; -1) làm vecto pháp tuyến
=> PT đi qua M (-2 ; -5) là
x + 2 - y - 5 = 0 ⇔ x - y - 3 = 0
b, c, Lười lắm ko làm đâu :)