Cho tam giác ABC cân tại A, có góc BAC nhọn. Qua A vẽ tia phân giác của góc BAC cắtcạnh BC tại D.a) Chứng minh ΔABD = ΔACD.b) Vẽ đường trung tuyến CF của tam giác ABC cắt cạnh AD tại G. Chứng minh G là trọngtâm của tam giác ABC.c) Gọi H là trung điểm của cạnh DC. Qua H vẽ đường thẳng vuông góc với cạnh DC cắtcạnh AC tại E. Chứng minh ΔDEC cân.d) Chứng minh ba điểm B, G, E thẳng hàng và AD > BDgiải...
Đọc tiếp
Cho tam giác ABC cân tại A, có góc BAC nhọn. Qua A vẽ tia phân giác của góc BAC cắt
cạnh BC tại D.
a) Chứng minh ΔABD = ΔACD.
b) Vẽ đường trung tuyến CF của tam giác ABC cắt cạnh AD tại G. Chứng minh G là trọng
tâm của tam giác ABC.
c) Gọi H là trung điểm của cạnh DC. Qua H vẽ đường thẳng vuông góc với cạnh DC cắt
cạnh AC tại E. Chứng minh ΔDEC cân.
d) Chứng minh ba điểm B, G, E thẳng hàng và AD > BD
giải họ giumf mình nha
giải câu d thôi nha các bạn
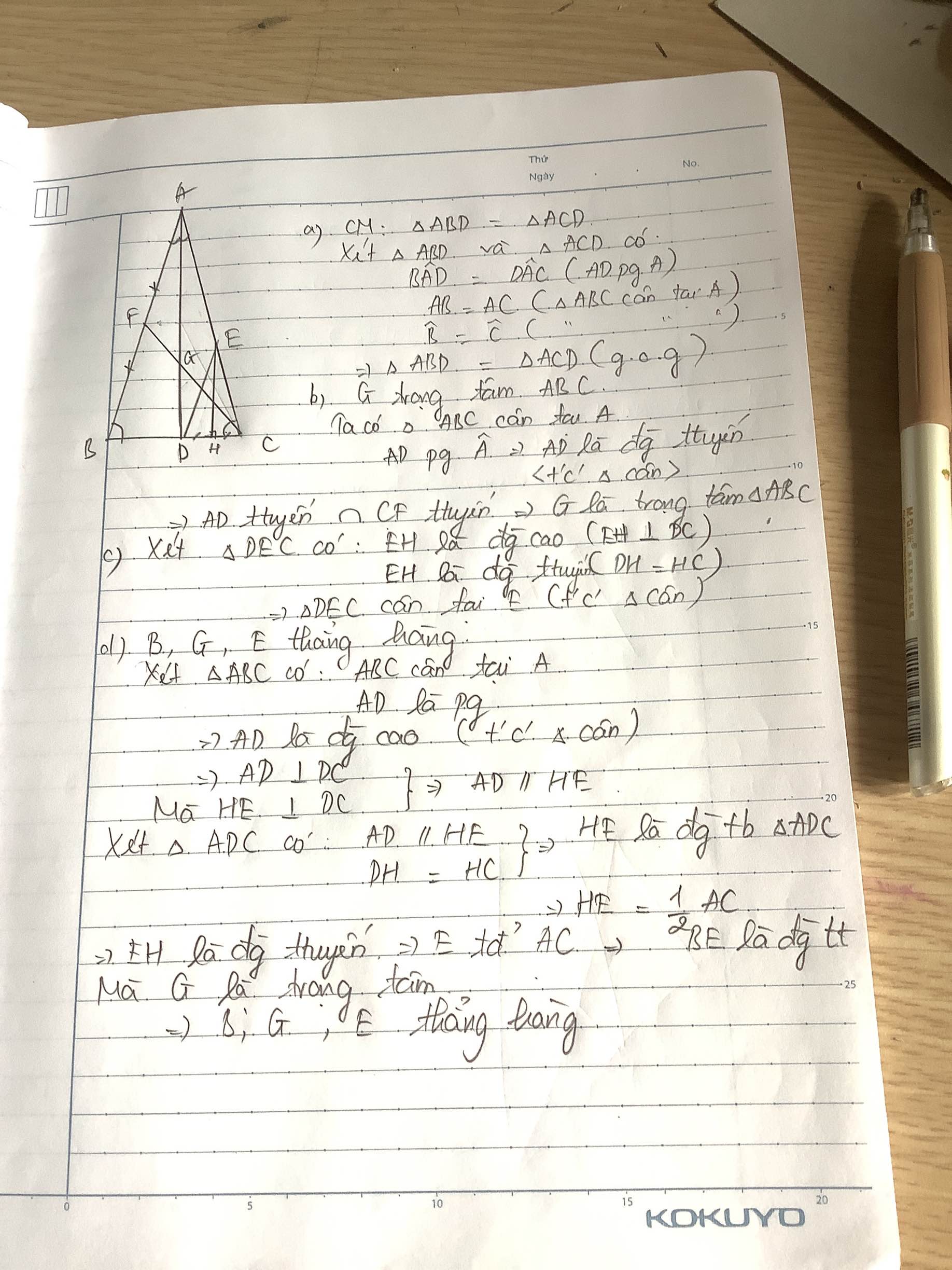
a)Xét \(\Delta ABCvà\Delta ACD\),ta có:
AB=AC(gt)
BAD=CDA(gt)
AD:chung
=>\(\Delta ABC=\Delta ACD\)(c,g.c)
Theo bài ra ta có AD//EH vậy từ đây suy ra gócADE=gócDEH (1)
Vì tam giácDEC cân => gocs EDC= gocsC= góc B (2)
Ta có: B+BAD=90 độ
EDC+DEH=90 độ
Vậy từ đây suy ra BAD=DEH.
Mà BAD=DAE(gt) và ADE=DEH (1)
Vậy từ đây suy ra DAE=ADE vậy từ đây suy ra tam giác ADE cân tại A vậy suy ra AE=DỄ mà DỄ=ẸC vậy suy ra AE=EC vậy suy ra E là trung điểm của AC
Vậy suy ra 3 điểm B,G,E thẳng hàng.
Còn cái AD>BD thì mình giải sau nhé. Không còn thời gian rồi