Cho góc tù xOy lấy điểm A thuộc tia Ox lấy điểm B thuộc tia Oy sao cho OA = OB. Đường vuông góc với OA tại A và đường vuông góc với OB tại B cắt nhau ở C.Gọi E là giao điểm của tia CA và tia đối của tia Oy.CHứng minh rằng:
a, OC là tia phân giác của góc xOy?
b, tam giác ODE là tam giác cân?
C, CO vuông góc với DE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 tháng 2 2019
tu ve hinh :
a, xet tamgiac OCB va tamgiac OCA co : OC chung
goc OBC = goc OAC = 90 do BC | Oy va AC | Ox (GT)
OB = OA (gt)
=> tamgiac OCB = tamgiac OCA (ch - cgv)
=> goc BOC = goc AOC (dn) ma OC nam giac Ox va Oy
=> OC la phan giac cua goc xOy (dn)
b, xet tamgiac OBD va tamgiac OAE co : OB = OA (gt)
goc BOD = goc AOE (doi dinh)
goc OBD = goc OAE = 90 do BC | Oy va AC | Ox (GT)
=> tamgiac OBD = tamgiac OAE (cgv - gnk)
=> OD = OE (dn)
=> tamgiac ODE can tai O (dn)
c, tu nghi di cau c-g-c
CM
11 tháng 8 2017
(h.114) Ta có CE = OD (câu a))
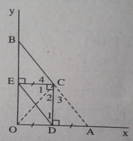
mà OD = DA (do D là trung điểm OA) nên CE = DA.
Xét ΔECD và ΔADC có:
CD chung
CE = DA( chứng minh trên)
∠(ECD) = ∠(CDA) = 90º
Do đó ΔECD = ΔADC (c.g.c)
⇒ ∠D1 = ∠C3 ⇒ CA // DE (hai góc so le trong bằng nhau).
CM
20 tháng 10 2019
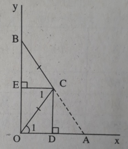
CD là đường trung trực của OA ⇒ CO = CA (tính chất đường trung trực) (1) .
CE là đường trung trực của OB ⇒ CO = CB (tính chất đường trung trực) (2).
Từ (1) và (2) suy ra: CA = CB.
17 tháng 2 2023
a: Xét ΔOAD và ΔOCB có
OA=OC
góc AOD chung
OD=OB
=>ΔOAD=ΔOCB
=>AD=CB
b: Xét ΔEAB và ΔECD có
góc EAB=góc ECD
AB=CD
góc EBA=góc EDC
=>ΔEAB=ΔECD
c: Xét ΔOAE và ΔOCE có
OA=OC
AE=CE
OE chung
=>ΔOAE=ΔOCE
=>góc AOE=góc COE
=>góc AOM=góc CON
Xét ΔCON và ΔAOM có
góc CON=góc AOM
CO=AO
góc OCN=góc OAM
=>ΔCON=ΔAOM
=>ON=OM
=>ΔENM can tại E
=>EM=EN
=>NC=MA
Xét ΔEMB và ΔEND có
EM=EN
góc MEB=góc NED
EB=ED
=>ΔEMB=ΔEND
=>ND=MB và góc EMB=góc END
=>góc KMO=góc KNO
=>ΔKMN cân tại K
KD+DN=KN
KB+BM=KM
mà KM=KN; DN=BM
nên KD=KB
=>K nằm trên trung trực của DB(1)
OB=OD
nên O nằm trên trung trực của DB(2)
EB=ED
nên E nằm trên trung trực của DB(3)
Từ (1), (2), (3) suy ra O,E,K thẳng hàng
CM
5 tháng 6 2018
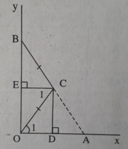
CD // OE (cùng vuông góc OA) ⇒ ∠(BEC) = ∠(ECD) (so le trong)
Ta lại có ∠(BEC) = 90o nên ∠(ECD) = 90o.
Vậy CE ⊥ CD.
CM
24 tháng 2 2017
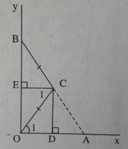
+) Vì CE // OD (cùng vuông góc với OB) ⇒ ∠C1 = ∠O1 (so le trong)
+) Xét ΔOCE và ΔCOD có:
OC chung
∠C1 = ∠O1 ( chứng minh trên )
∠OEC = ∠ODC = 90º
Suy ra: ΔOCE = ΔCOD (cạnh huyền – góc nhọn) ⇒ CE = OD.
CM
13 tháng 5 2017
Cách 1: Theo câu d): CA // DE. Chứng minh tương tự: CB // DE.
Qua C ta có CA và CB cùng song song với DE nên theo tiên đề Ơ-clit: A, C, B thẳng hàng.
Cách 2. CO = CA ⇒ ΔOCA cân ⇒ đường cao CD là đường phân giác của góc OCA ⇒ ∠C2 = ∠C3 ⇒ ∠(OCA) = 2∠C2 .
Chứng minh tương tự: ∠C1 = ∠C4 ⇒ ∠(OCB) = 2∠C1.
Do đó:
∠(OCA) + ∠(OCB) = 2∠C2 + 2∠C1 = 2(∠C2 + ∠C1) = 2∠(ECD) = 2.90o = 180o.
Vậy A, C, B thẳng hàng.