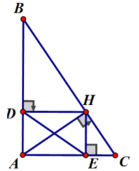
Cho \(\Delta ABC\)cân tại A có đường cao AH, kẻ HI vuông góc với AC tại I
a) Chứng minh \(\Delta ABC\)đồng dạng với \(\Delta CHI\)
b) Chứng minh \(AH^2\)= AC.AI
C) Gọi D là trung điểm của HI. Chứng minh \(\widehat{DAH}=\widehat{IBC}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ Xét \(\Delta ABC\) và \(\Delta HAC\) có :
\(\left\{{}\begin{matrix}\widehat{C}chung\\\widehat{BAC}=\widehat{AHC}=90^0\end{matrix}\right.\)
\(\Leftrightarrow\Delta ABC\sim HAC\left(g-g\right)\)
b/ \(BC=\sqrt{AB^2+AC^2}=10cm\)
\(AH.BC=AB.AC\Leftrightarrow AH=\dfrac{AB.AC}{BC}=4,8cm\)
c/ \(\Delta HEA\sim\Delta CEH\left(g-g\right)\)
\(\Leftrightarrow\dfrac{HE}{CE}=\dfrac{EA}{HE}\Leftrightarrow HE^2=EA.EC\left(đpcm\right)\)
a) Xét ΔHAC và ΔABC có:
∠(ACH ) là góc chung
∠(BAC)= ∠(AHC) = 90o
⇒ ΔHAC ∼ ΔABC (g.g)
b) Xét ΔHAD và ΔBAH có:
∠(DAH ) là góc chung
∠(ADH) = ∠(AHB) = 90o
⇒ ΔHAD ∼ ΔBAH (g.g)

c) Tứ giác ADHE có 3 góc vuông ⇒ ADHE là hình chữ nhật.
⇒ ΔADH= ΔAEH ( c.c.c) ⇒ ∠(DHA)= ∠(DEA)
Mặt khác: ΔHAD ∼ ΔBAH ⇒ ∠(DHA)= ∠(BAH)
∠(DEA)= ∠(BAH)
Xét ΔEAD và ΔBAC có:
∠(DEA)= ∠(BAH)
∠(DAE ) là góc chung
ΔEAD ∼ ΔBAC (g.g)
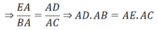
d) ΔEAD ∼ ΔBAC
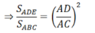
ΔABC vuông tại A, theo định lí Pytago:
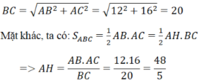
Theo b, ta có:
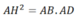
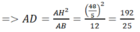
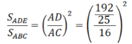

a) Xét ΔDAH vuông tại D và ΔHAC vuông tại H có
\(\widehat{DAH}\) chung
Do đó: ΔDAH\(\sim\)ΔHAC(g-g)

Câu 1:
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc BAD chung
DO đo: ΔADB đồng dạng với ΔAEC
Suy ra: AD/AE=AB/AC
hay AD/AB=AE/AC
b: Xét ΔADE và ΔABC có
AD/AB=AE/AC
góc DAE chung
Do đó: ΔADE đồng dạng với ΔABC
Suy ra: DE/BC=AD/AB
hay \(DE\cdot AB=AD\cdot BC\)
c: Xét ΔOBE và ΔODC có
góc OBE=góc ODC
góc BOE chung
Do đo: ΔOBE đồng dạng với ΔODC
Suy ra: OB/OD=OE/OC
hay \(OB\cdot OC=OE\cdot OD\)

a)xét ΔABC và ΔHBA ta có
\(\widehat{BAH}=\widehat{BHA}=90^o\)
\(\widehat{B}chung\)
=>ΔABC ∼ ΔHBA(g.g)(1)
b)xét ΔABC và ΔAHC ta có
\(\widehat{BAC}=\widehat{AHC}=90^o\)
\(\widehat{B}chung\)
->ΔABC ∼ ΔAHC(g.g)(2)
từ (1) và (2)=>ΔHBA và ΔAHC
->\(\dfrac{AH}{BH}=\dfrac{HC}{AH}\)
=>\(AH^2=BH.HC\)

ttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttt
a)
Xét \(\Delta\)ABC và \(\Delta\)HBA có:
^BAC = ^BHA ( = 90 độ )
^ABC = ^HBA ( ^B chung )
=> \(\Delta\)ABC ~ \(\Delta\)HBA
b) AB = 3cm ; AC = 4cm
Theo định lí pitago ta tính được BC = 5 cm
Từ (a) => \(\frac{AB}{BH}=\frac{BC}{AB}\Rightarrow BH=\frac{AB^2}{BC}=1,8\)m
c) Xét \(\Delta\)AHC và \(\Delta\)AKH có: ^AKH = ^AHC = 90 độ
và ^HAC = ^HAK ( ^A chung )
=> \(\Delta\)AHC ~ \(\Delta\)AKH
=> \(\frac{AH}{AK}=\frac{AC}{AH}\Rightarrow AH^2=AC.AK\)
d) Bạn kiểm tra lại đề nhé!

a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
\(\widehat{BAD}\) chung
Do đó: ΔADB\(\sim\)ΔAEC
b: Xét ΔEHB vuông tại E và ΔDHC vuông tại H có
\(\widehat{EHB}=\widehat{DHC}\)
Do đó: ΔEHB\(\sim\)ΔDHC
Suy ra: \(\dfrac{HE}{HD}=\dfrac{HB}{HC}\)
hay \(HE\cdot HC=HB\cdot HD\)
c: Xét tứ giác HBKC có
HB//KC
HC//BK
Do đó: HBKC là hình bình hành
Suy ra: Hai đường chéo HK và BC cắt nhau tại trung điểm của mỗi đường
mà M là trung điểm của BC
nên M là trung điểm của HK
hay H,M,K thẳng hàng