Tìm các số nguyên x, y sao cho: a) x . y = 5; b) x . y = 8
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
24 tháng 7 2018
Đúng(0)
Những câu hỏi liên quan
9 tháng 2 2021
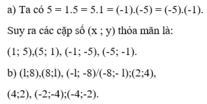
a) Ta có: (x-3)(y+2)=5
nên (x-3) và (y+2) là ước của 5
\(\Leftrightarrow x-3;y+2\in\left\{1;-5;-1;5\right\}\)
Trường hợp 1:
\(\left\{{}\begin{matrix}x-3=1\\y+2=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=3\end{matrix}\right.\)
Trường hợp 2:
\(\left\{{}\begin{matrix}x-3=5\\y+2=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=8\\y=-1\end{matrix}\right.\)
Trường hợp 3:
\(\left\{{}\begin{matrix}x-3=-1\\y+2=-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=-7\end{matrix}\right.\)
Trường hợp 4:
\(\left\{{}\begin{matrix}x-3=-5\\y+2=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=-3\end{matrix}\right.\)
Vậy: \(\left(x,y\right)\in\left\{\left(4;3\right);\left(8;-1\right);\left(2;-7\right);\left(-2;-3\right)\right\}\)
b) Ta có: (x-2)(y+1)=5
nên x-2 và y+1 là các ước của 5
\(\Leftrightarrow x-2;y+1\in\left\{1;-1;5;-5\right\}\)
Trường hợp 1:
\(\left\{{}\begin{matrix}x-2=1\\y+1=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=4\end{matrix}\right.\)
Trường hợp 2:
\(\left\{{}\begin{matrix}x-2=5\\y+1=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=7\\y=0\end{matrix}\right.\)
Trường hợp 3:
\(\left\{{}\begin{matrix}x-2=-1\\y+1=-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-6\end{matrix}\right.\)
Trường hợp 4:
\(\left\{{}\begin{matrix}x-2=-5\\y+1=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-3\\y=-2\end{matrix}\right.\)
Vậy: \(\left(x,y\right)\in\left\{\left(3;4\right);\left(7;0\right);\left(1;-6\right);\left(-3;-2\right)\right\}\)
PT
1
CM
8 tháng 11 2018
a) Ta có 5 = 1.5 = 5.1 = (-1).(-5) = (-5).(-1).
Suy ra các cặp số (x ; y) thỏa mãn là:
(1; 5),(5; 1), (-1; -5), (-5; -1).
b) (l;8),(8;l), (-l; -8)/(-8;- l);(2;4), (4;2), (-2;-4);(-4;-2).
PT
1
CM
14 tháng 5 2019
Viết số -5 thành tích của hai số nguyên theo tất cả các cách, ta có:
-5 = l.(-5)=(-5).l = (-l).5 = 5.(-l). Từ đó ta tìm được x,y thỏa mãn điều kiện đề bài.
a) Các cặp số (x ; y) tìm được là: (1;-5),(-5; 1), (-1;5),(5; -1)
b) Dựa vào câu a và kết hợp điều kiện x > y, ta tìm được các cặp số (x;y) sau: (5;-l),(l;-5).
c) Làm tương tự câu a, ta tìm được x + 1 và y - 2. Từ đó suy ra (x;y) là (0;-3), (-6; 3), (-2; 7), (4; 1).
PT
1
CM
15 tháng 2 2017
Viết số -5 thành tích của hai số nguyên theo tất cả các cách, ta có: -5 = l.(-5)=(-5).l = (-l).5 = 5.(-l). Từ đó ta tìm được x,y thỏa mãn điều kiện đề bài. a) Các cặp số (x ; y) tìm được là: (1;-5),(-5; 1), (-1;5),(5; -1) b) Dựa vào câu a và kết hợp điều kiện x > y, ta tìm được các cặp số (x;y) sau: (5;-l),(l;-5). c) Làm tương tự câu a, ta tìm được x + 1 và y - 2. Từ đó suy ra (x;y) là (0;-3), (-6; 3), (-2; 7), (4; 1)
T
28 tháng 11 2023
Giup mình với ah.
1- Tính :
A= 5. | x- 5 | - 3x + 1
2 - Tìm các số nguyên x,y ; sao cho :
a) 5/x - y/3 = 1/6 b) 5/x + y/4 = 1/8
3- Tìm giá trị lớn nhất của Q = 27-2x/12-x ( x là số nguyên)
---------------------------------------------------------------------------------------------
12 tháng 7 2023
2:
a: 5/x-y/3=1/6
=>\(\dfrac{15-xy}{3x}=\dfrac{1}{6}\)
=>\(\dfrac{30-2xy}{6x}=\dfrac{x}{6x}\)
=>30-2xy=x
=>x(2y+1)=30
=>(x;2y+1) thuộc {(30;1); (-30;-1); (10;3); (-10;-3); (6;5); (-6;-5)}
=>(x,y) thuộc {(30;0); (-30;-1); (10;1); (-10;-2); (6;2); (-6;-3)}
b: x/6-2/y=1/30
=>\(\dfrac{xy-12}{6y}=\dfrac{1}{30}\)
=>\(\dfrac{5xy-60}{30y}=\dfrac{y}{30y}\)
=>5xy-60=y
=>y(5x-1)=60
=>(5x-1;y) thuộc {(-1;-60); (4;15); (-6;-10)}(Vì x,y là số nguyên)
=>(x,y) thuộc {(0;-60); (1;15); (-1;-10)}
28 tháng 11 2023
1) \(A=5.\left|x-5\right|-3x+1\)
\(A=\left[{}\begin{matrix}5.\left(x-5\right)-3x+1\left(x-5\ge0\right)\\5.\left(5-x\right)-3x+1\left(x-5< 0\right)\end{matrix}\right.\)
\(A=\left[{}\begin{matrix}5x-25-3x+1\left(x\ge5\right)\\25-5x-3x+1\left(x< 5\right)\end{matrix}\right.\)
\(A=\left[{}\begin{matrix}2x-24\left(x\ge5\right)\\26-8x\left(x< 5\right)\end{matrix}\right.\)
29 tháng 11 2023
3:
\(Q=\dfrac{27-2x}{12-x}=\dfrac{2x-27}{x-12}\)
\(\Leftrightarrow Q=\dfrac{2x-24-3}{x-12}=2-\dfrac{3}{x-12}\)
Để Q lớn nhất thì \(2-\dfrac{3}{x-12}\) lớn nhất
=>\(\dfrac{3}{x-12}\) nhỏ nhất
=>x-12 là số nguyên âm lớn nhất
=>x-12=-1
=>x=11
Vậy: \(Q_{min}=2-\dfrac{3}{11-12}=2+3=5\) khi x=11
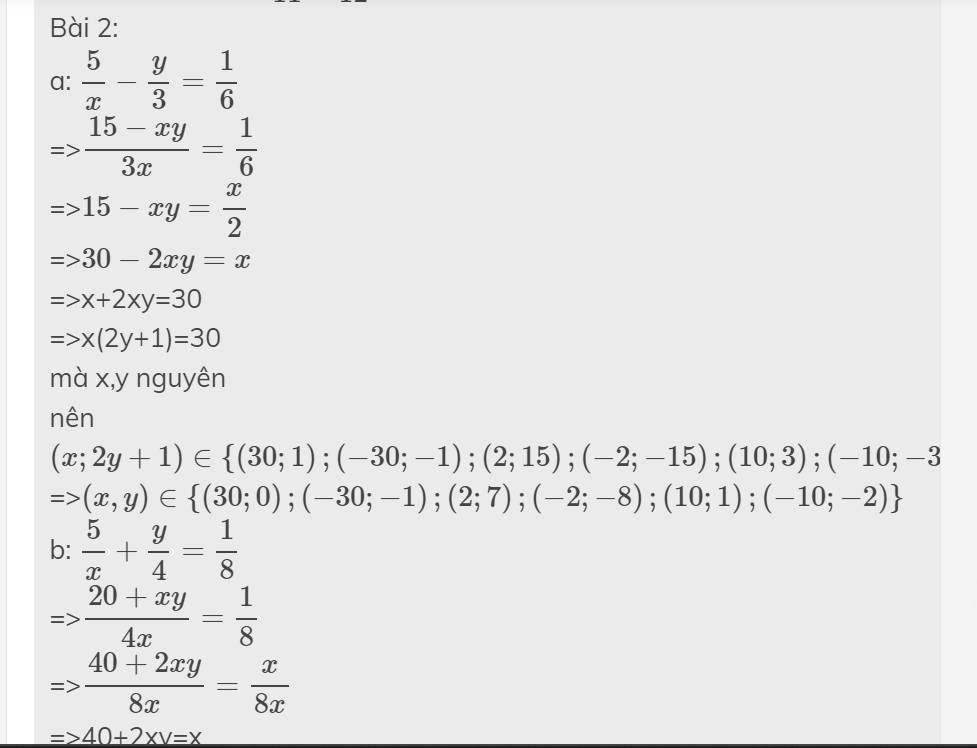
Bài 2:
a: \(\dfrac{5}{x}-\dfrac{y}{3}=\dfrac{1}{6}\)
=>\(\dfrac{15-xy}{3x}=\dfrac{1}{6}\)
=>\(15-xy=\dfrac{x}{2}\)
=>\(30-2xy=x\)
=>x+2xy=30
=>x(2y+1)=30
mà x,y nguyên
nên \(\left(x;2y+1\right)\in\left\{\left(30;1\right);\left(-30;-1\right);\left(2;15\right);\left(-2;-15\right);\left(10;3\right);\left(-10;-3\right)\right\}\)
=>\(\left(x,y\right)\in\left\{\left(30;0\right);\left(-30;-1\right);\left(2;7\right);\left(-2;-8\right);\left(10;1\right);\left(-10;-2\right)\right\}\)
b: \(\dfrac{5}{x}+\dfrac{y}{4}=\dfrac{1}{8}\)
=>\(\dfrac{20+xy}{4x}=\dfrac{1}{8}\)
=>\(\dfrac{40+2xy}{8x}=\dfrac{x}{8x}\)
=>40+2xy=x
=>x-2xy=40
=>x(1-2y)=40
mà x,y nguyên
nên \(\left(x;1-2y\right)\in\left\{\left(40;1\right);\left(-40;-1\right);\left(8;5\right);\left(-8;-5\right)\right\}\)
=>\(\left(x,y\right)\in\left\{\left(40;0\right);\left(-40;1\right);\left(8;-2\right);\left(-8;3\right)\right\}\)