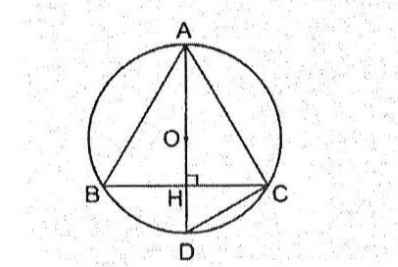
Cho tam giác ABC cân tại A nội tiếp trong đường tròn (O;R) có AB = R.
a, CMR: AO là tia phân giác của góc BAC
b, C/tỏ BC > R. So sánh khoảng cách từ tâm O đến các cạnh của tam giác ABC.
c, Tính theo R độ dài cạnh BC và chiều cao AH hạ từ A đến BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MH
5 tháng 2 2022
Tham khảo:
Ta có: \(R=\dfrac{abc}{4S};r=\dfrac{S}{p}\)
Vì tam giác ABC vuông cân tại A nên \(b=c\) và \(a=\sqrt{b^2+c^2}=b\sqrt{2}\)
Xét tỉ số:
\(\dfrac{R}{r}=\dfrac{abc.p}{4S^2}=\dfrac{abc.\dfrac{a+b+c}{2}}{4.\dfrac{1}{4}.\left(b.c\right)^2}=\dfrac{a\left(a+2b\right)}{2b^2}=\dfrac{2b^2\left(1+\sqrt{2}\right)}{2b^2}=1+\sqrt{2}\)
19 tháng 2 2022
a: Xét tứ giác ABDE có
\(\widehat{ADB}=\widehat{AEB}=90^0\)
Do đó: ABDE là tứ giác nội tiếp
b: Xét ΔDAC vuông tại D và ΔDBF vuông tại D có
\(\widehat{DAC}=\widehat{DBF}\)
Do đó:ΔDAC∼ΔDBF
Suy ra: DA/DB=DC/DF
hay \(DB\cdot DC=DA\cdot DF\)
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 8 2021
Kéo dài AH cắt đường tròn tại D \(\Rightarrow\) AD là đường kính
\(\Rightarrow\widehat{ABD}\) là góc nội tiếp chắn nửa đường tròn hay tam giác ABD vuông tại B
Áp dụng hệ thức lượng:
\(AB^2=AH.AD\Rightarrow AD=\dfrac{AB^2}{AH}=\dfrac{b^2}{h}\)
\(\Rightarrow2R=\dfrac{b^2}{h}\Rightarrow R=\dfrac{b^2}{2h}\)
16 tháng 3 2023
a: góc HMC+góc HNC=180 độ
=>HMCN nội tiếp
b: góc CAD=góc NBC
=>1/2*sđ cung CD=1/2*sđ cung CE
=>CD=CE
c: góc BHM=góc BCN=1/2*sđ cung BA
góc BDH=1/2*sđ cung BA
=>góc BHD=góc BDH
=>ΔBHD cân tại B
TS
14 tháng 7 2021
Kẻ đường kính AD thì góc ACD = 90°
Ta có AC²= AD.AH nên AD = AC²/AH
<=>AD= (10a)²/ 8a=100a/8