Cho tam giác ABC.Â=90o..Kẻ AH vuôg BK;HD vuôg AB,HE vuôg AC.CMR:
\(\dfrac{AB^2}{AB^2}=\dfrac{HB}{HC}\)
\(\dfrac{AB^3}{AC^3}=\dfrac{BD}{EC}\)
\(BC^2=3AH^2+BD^2+CE^2\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PN
2
HP
18 tháng 2 2016
Tự vẽ hình
Ta có tam giác ABC đều<=>AB=BC=AC
Vì AH _|_ BC=> tam giác AHB và tam giác AHC vuông tại H
Xét tam giác AHB và tam giác AHC (vuông tại H) có:
AH: cạnh chung
AB=AC(chứng minh trên)
=>tam giác...=tam giác...( cạnh huyền-cạnh góc vuông)
=> góc HAB=góc HAC( cặp góc tương ứng)(1)
Mà góc AHB + góc AHC=góc BAC=60 đo( do tam giác ABC đều)(2)
Từ (1);(2)=>góc HAB=60 đo/2=30 đo
18 tháng 2 2016
xét tam giác vuông AHB và tam giác vuông AHC ,có
AH: cạnh chung
AB=AC (gt)
do đó tam giác vuông AHB = tam giác vuông AHC (cạnh huyền-cạnh góc vuông)
suy ra: góc HAB = góc HAC (2 góc tương ứng)
mà : góc A = 600
nên góc HAB = 600 :2 = 300
vậy góc HAB = 300
16 tháng 7 2015
Câu a thì em sử dụng trường hợp = nhau trong tam giác [c.g.c]
Câu b:
1. chứng minh cho PHAQ là HCN [tứ giác có 3 góc vuông]
2. Từ HCN PHQA => PH=AQ [MÀ PH=PE ->PE=AQ] , PA=HQ[mà HQ=QF -> QF=PA] rồi xét 2 tam giác PAE = QFA[c.g.c]
Hai tam giác bằng nhau => AE=AF mà A thuộc EF => A là trung điểm của EF
NT
Cho tam giác abc, cân tại a. Kẻ ah vuôg góc vs bc ( h thuộc bc)
a) biết ah=4cm,ab=5cm. Tính độ dài bh
3
VN
23 tháng 4 2017
Cách 1: Dùng pytago với tgiác ABH => BH luôn
Cách 2: Dùng pytago với tgiác ACH => HC
Mà phải cm H là trung điểm BC nữa => HB. Nhưng cminh cũng không có gì khó khăn đâu mà
Nên tốt nhất bạn chọn cách 1 đi.
23 tháng 4 2017
Vì \(AH⊥BC\Rightarrow\Delta AHB\) là tam giác vuông
Vì \(\Delta AHB\) vuông \(\Rightarrow AB^2=AH^{^{ }2}+BH^{^{ }2}\left(Py-ta-go\right)\)
hay \(^{5^2=4^2+BH^2}\)
\(5^2-4^2=BH^2\)
\(25-16=BH^2\)
\(9=BH^2\Rightarrow BH=\sqrt{9}\Rightarrow BH=3cm\)
Vậy BH=3cm
CM
23 tháng 8 2017
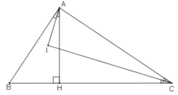
Ta có: AH⊥BC (gt) ⇒ ΔAHB vuông tại H
Trong tam giác vuông AHB ta có: ∠BHA = 90o
⇒ ∠B + ∠BAH = 90o (1)
Trong tam giác vuông ABC ta có: ∠BAC = 90o
⇒ ∠B + ∠C = 90o (2)
Từ (1) và (2) suy ra: ∠BAH = ∠C (3)
+) Vì AI là tia phân giác của góc BAC nên:
∠(BAI) = ∠(IAH) = 1/2.∠BAH (4)
Do CI là tia phân giác của góc ACB nên:
∠(ACI) = ∠(ICB) = 1/2.∠C (5)
+) Từ (3); (4) và (5) suy ra:
∠(BAI) = ∠(IAH) = ∠(ACI) = ∠(ICB)
+) Lại có:
∠BAI + ∠IAC = 90º
Suy ra: ∠ICA + ∠IAC = 90º
Trong ΔAIC có: ∠ICA+ ∠IAC = 90º
Vậy: ∠AIC = 90º.
28 tháng 3 2023
a: ΔBCA cân tạiA
mà AH là đường cao
nên AH là phân giác
b: Xet ΔBMI vuông tại M và ΔBHI vuông tại H có
BI chung
góc MBI=góc HBI
=>ΔBMI=ΔBHI
=>IM=IH
Xét ΔIMA vuông tại M và ΔINA vuông tại N có
AI chung
góc MAI=góc NAI
=>ΔIMA=ΔINA
=>IM=IN=IH
c: Xet ΔIMA vuông tại M và ΔINA vuông tại N có
AI chung
góc MAI=góc NAI
=>ΔIMA=ΔINA
=>góc MIA=góc NIA
=>IA là phân giác của góc MIN
5 tháng 5 2021
b) Ta có: KI\(\perp\)BC(gt)
AH\(\perp\)BC(gt)
Do đó: KI//AH(Định lí 1 từ vuông góc tới song song)
Suy ra: \(\widehat{HAI}=\widehat{KIA}\)(hai góc so le trong)(1)
Ta có: ΔABK=ΔIBK(cmt)
nên KA=KI(hai cạnh tương ứng)
Xét ΔKAI có KA=KI(cmt)
nên ΔKAI cân tại K(Định nghĩa tam giác cân)
Suy ra: \(\widehat{KAI}=\widehat{KIA}\)(hai góc ở đáy)(2)
Từ (1) và (2) suy ra \(\widehat{HAI}=\widehat{KAI}\)
\(\Leftrightarrow\widehat{HAI}=\widehat{CAI}\)
Suy ra: AI là tia phân giác của \(\widehat{HAC}\)(Đpcm)
5 tháng 5 2021
a) Xét ΔABK vuông tại A và ΔIBK vuông tại I có
BK chung
\(\widehat{ABK}=\widehat{IBK}\)(BK là tia phân giác của \(\widehat{ABI}\))
Do đó: ΔABK=ΔIBK(Cạnh huyền-góc nhọn)
a: \(\dfrac{AB^2}{AC^2}=\dfrac{HB\cdot BC}{HC\cdot BC}=\dfrac{HB}{HC}\)
b: \(\dfrac{BD}{CE}=\dfrac{BH^2}{AB}:\dfrac{CH^2}{AC}=\dfrac{BH^2}{CH^2}\cdot\dfrac{AC}{AB}=\dfrac{AB^4}{AC^4}\cdot\dfrac{AC}{AB}=\dfrac{AB^3}{AC^3}\)