3. Cho tam giác ABC vuông tại A, có:
a) C = 60độ; BC =16. Tính AB, AC
b) C = 60độ; AB= 5 căng3. Tính BC, AC
4. Cho tam giác ABC vuông tại A, biết cosB = 0,8. Tính các tỉ số lượng giác của góc C.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
2 tháng 2 2019
Chọn B
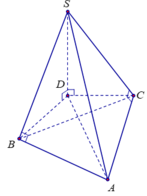
Gọi D là hình chiếu của S lên mặt phẳng (ABC), suy ra S D ⊥ A B C .
Ta có S D ⊥ A B và S B ⊥ A B ( g t ) , suy ra A B ⊥ S B D ⇒ B A ⊥ B D .
Tương tự có A C ⊥ D C hay tam giác ACD vuông ở C.
Dễ thấy ∆ S B A = ∆ S C A (cạnh huyền và cạnh góc vuông), suy ra SB=SC. Từ đó ta chứng minh được ∆ S B D = ∆ S C D nên cũng có DB=DC.
Vậy DA là đường trung trực của BC, nên cũng là đường phân giác của góc B A C ^ .
Ta có
D
A
C
^
=
30
o
, suy ra
D
C
=
a
3
. Ngoài ra góc giữa hai mặt phẳng (SAB) và (ABC) là
S
B
D
^
=
60
o
suy ra
tan
S
B
D
^
=
S
D
B
D
⇒
S
D
=
B
D
tan
S
B
D
^
=
a
3
.
3
=
a
Vậy
V
S
.
A
B
C
=
1
3
.
S
∆
A
B
C
.
S
D
=
1
3
a
2
3
4
.
a
=
a
3
3
12
22 tháng 4 2015
a) Xét \(\Delta HAC\) và \(\Delta ABC\) có :
Góc AHC = góc BAC = 90o; góc C chung
=> \(\Delta HAC\) đồng dạng với \(\Delta ABC\) (g.g)
b) Vì \(\Delta ABC\) vuông tại A nên AB2 + AC2 = BC2 => AB2 = BC2 - AC2 = 202 - 162 = 144
=> \(AB=\sqrt{144}=12\left(cm\right)\)
Từ a) => \(\frac{AH}{AB}=\frac{AC}{BC}\) hay \(\frac{AH}{6}=\frac{8}{10}\) => \(AH=\frac{6.8}{10}=4,8\left(cm\right)\)
c) Ta có \(\Delta ABD\) đồng dạng với \(\Delta HBI\) (g.g) ('Bạn tự chứng minh')
=> Góc BIH = góc ADB
Mà góc BIH = góc AID (đ2) => Góc AID = góc ADB
=> Tam giác AID cân tại A
d) ('Mình ko biết')
28 tháng 7 2016
a) Xét \(\Delta HAC\) và \(\Delta ABC\) có :
Góc AHC = góc BAC = 90o; góc C chung
=> \(\Delta HAC\) đồng dạng với \(\Delta ABC\) (g.g)
b) Vì \(\Delta ABC\) vuông tại A nên AB2 + AC2 = BC2 => AB2 = BC2 - AC2 = 202 - 162 = 144
=> \(AB=\sqrt{144}=12\left(cm\right)\)
Từ a) => \(\frac{AH}{AB}=\frac{AC}{BC}\) hay \(\frac{AH}{6}=\frac{8}{10}\) => \(AH=\frac{6.8}{10}=4,8\left(cm\right)\)
c) Ta có \(\Delta ABD\) đồng dạng với \(\Delta HBI\) (g.g) ('Bạn tự chứng minh')
=> Góc BIH = góc ADB
Mà góc BIH = góc AID (đ2) => Góc AID = góc ADB
=> Tam giác AID cân tại A