Cho hình thang ABCD(AB/CD và góc DAB =góc DBC) iết AB=2,5cm;AD=3,5cm;BD=5cm
a) Chứng minh tam giác ABD ~ tam giác BDC
b) Tính độ dài các cạnh của BC và CD
c) Chứng minh \(\frac{S_{ABD}}{S_{BDC}}\)= 1/4
AI GIÚP VS HELP ME
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
22 tháng 7 2018
Vì
△
ABD ∼
△
BDC nên: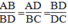 
Với AB = 2,5cm; AD = 3,5cm; BD = 5cm, ta có:
5 tháng 5 2020
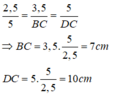
câu hỏi ko rõ tìm x là tìm góc hay cạnh, chu vi, diện tích
30 tháng 4 2023
a: Xét ΔDAB và ΔCBD có
góc DAB=góc CBD
góc ABD=góc BDC
=>ΔDAB đồng dạng với ΔCBD
b: ΔDAB đồng dạng với ΔCBD
=>DA/CB=DB/CD=AB/BD
=>3/4=DB/CD=5/BD
=>BD=5:3/4=20/3cm; DB^2=5*CD
=>5*CD=400/9
=>CD=80/9cm
CM
18 tháng 8 2019
Vẽ hình thang ABCD
- B1: Vẽ tam giác ABD theo độ dài cho trước của mỗi cạnh
- B2: Lấy B làm tâm, quay cung tròn có bán kính 7cm, rồi lấy D làm tâm quay cung tròn có bán kính 10cm, hai cung này cắt nhau tại điểm C ( khác phía với A so với BD)
2 tháng 3 2022
a: Xét ΔADB và ΔBCD có
\(\widehat{BAD}=\widehat{DBC}\)
\(\widehat{ABD}=\widehat{BDC}\)
Do đó: ΔADB\(\sim\)ΔBCD
b: ta có:ΔADB\(\sim\)ΔBCD
nên AD/BC=AB/BD
=>2,5/BC=1/2
hay BC=5(cm)
CM
13 tháng 5 2017
Xét △ ABD và △ BDC, ta có:
∠ (DAB) = ∠ (DBC) (gt)
∠ (ABD) = ∠ (BDC) (so le trong)
Suy ra: △ ABD ∼ △ BDC (g.g)