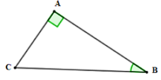
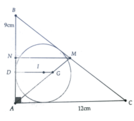
Cho tam giác ABC vuông tại A , có AB = 12 cm ; AC = 16cm . Kẻ đường cao AH ( H ∈ BC )
a) Chứng minh ▲HBA đồng dạng ▲ABC
b) Tính độ dài các đoạn thẳng BC , AH
c ) Trong ▲ABC kẻ phân giác AD ( D∈ BC ) . Trong ▲ADB kẻ phân giác DE ( E ∈ AB) trong ▲ADC kẻ phân giác DF ( F ∈ AC )
Chứng minh ràng : \(\dfrac{EA}{EB}\) . \(\dfrac{DB}{DC}\) . \(\dfrac{FC}{FA}\) = 1



a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
b: BC=căn 12^2+16^2=20cm
AH=12*16/20=9,6cm