Trong không gian với hệ tọa độ Oxyz, cho điểm M (2;-1;0).
Hỏi có bao nhiêu mặt phẳng (P) đi qua M và cắt các trục Ox,
Oy, Oz lần lượt tại các điểm A, B, C sao cho O A = 2 O B = 3 O C ≠ 0 ?
![]()
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
Ta có phương trình mặt phẳng (P) đi qua M và vuông góc với d
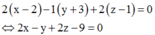
Gọi I là giao điểm của đường thẳng d và (P) khi đó tạo độ I là nghiệm của hệ
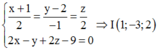
M’ đối xứng với M qua d thì I là trung điểm của MM’ ⇒ M’(0;-3;3)

Chọn C
Gọi I là trung điểm của 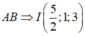
Ta có: ![]()
![]()
IA²+IB² không đổi nên MA²+MB² đạt giá trị nhỏ nhất khi MI đạt giá trị nhỏ nhất.
=> M là hình chiếu của I trên trục Oz.
=> M (0;0;3).

Chọn C
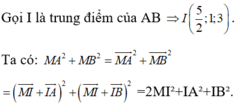
IA²+IB² không đổi nên MA²+MB² đạt giá trị nhỏ nhất khi MI đạt giá trị nhỏ nhất.
Suy ra M là hình chiếu của I trên trục Oz.
Suy ra M (0;0;3).

Chọn C
Gọi I là trung điểm của AB 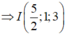
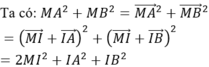
Suy ra: MA2 + MB2 đạt giá trị nhỏ nhất khi MI đạt giá trị nhỏ nhất.
=>M là hình chiếu của I trên trục Oz => M (0 ; 0 ; 3)
Đáp án C