Cho Δ ABC có góc A = 60 độ. Tia pg của góc B cắt AC tại E; tia pg của góc C cắt AB tại F.C/m: BF +...
Đọc tiếp
Cho Δ ABC có góc A = 60 độ. Tia pg của góc B cắt AC tại E; tia pg của góc C cắt AB tại F.C/m: BF + CE=BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AA
0
AA
0
KP
20 tháng 4 2022
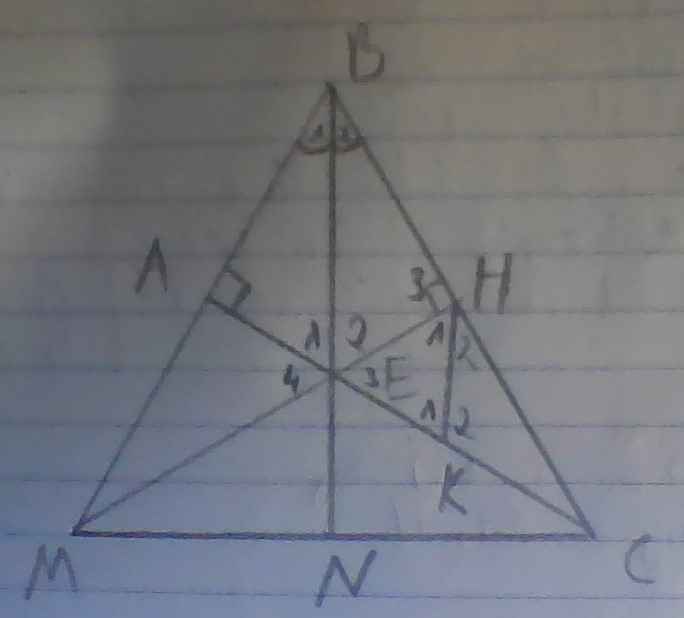
a) có BE là tia p/g của góc ABC
=> góc B1 = góc B2 = góc ABC/2 = 600 /2 = 300
có △ABC vuông tại A => △ABE vuông tại A
EH⊥BC=> △HBE vuông tại H
Xét △ vuông ABE và △vuông HBE có
góc B1 = góc B2
BE chung
=>△ vuông ABE =△vuông HBE ( cạnh huyền - góc nhọn)
b) có △ABE vuông tại A=> góc B1 + góc E1 = 900
góc E1 = 600 ( vì góc B1 = 300)
có △ vuông ABE =△vuông HBE
=> góc E1 = góc E2
mà HK//BE => góc E1 = góc K1 (ĐV)
và góc E2 = góc H1 (SLT)
=> góc E1 = góc E2 = góc K1=góc H1 = 600
=> △HEK đều
c) có góc E1 = góc E2 ; góc E3 = góc E4
=>góc E1 +góc E4 = góc E2 + góc E3
=> góc BEM= góc BEC
Xét △BEM và △ BEC có
góc B1 = góc B2
BE chung
góc BEM= góc BEC
=> △BEM = △ BEC (g.c.g)
=>BM=BC
=>△BMC cân tại B
trong △BMC có BN là đường p/g xuất phát từ đỉnh B
lại có △BMC cân tại B
=> BN cũng là đường trung tuyến xuất phát từ đỉnh B
=> N là trung điểm của MC
=> NM=NC
10 tháng 3 2019
M A C B N K I 1 2 1 2 3 4 1 2 60 0
Xét \(\Delta ABC\)có:
\(\widehat{ABC}+\widehat{BCA}=180^0-60^0=120^0\)
mÀ \(\widehat{B_1}=\widehat{B_2}\)(TIA pg)
\(\widehat{C_1}=\widehat{C_2}\left(pg\right)\)
\(\Rightarrow\widehat{B_2}+\widehat{C_2}=\frac{1}{2}\left(\widehat{B}+\widehat{C}\right)=60^0\)
\(\Rightarrow\widehat{BIC}=120^0\)
Kẻ IK là pg \(\widehat{BIC}\)
\(\Rightarrow\widehat{I_2}=\widehat{I_3}\left(=60^0\right)\)
T a có: \(\widehat{I_4}=\widehat{I_1}=180^0-\widehat{BIC}=60^0\)
\(\Rightarrow\widehat{I_1}=\widehat{I_2}=\widehat{I_3}=\widehat{I_4}\left(=60^0\right)\)
Xét tam giác BNI=tam giác BKI(g.c.g) có:
BN=BK(2 cạnh t/ư)
Tương tự ta c/m đc tam giác IKC= tam giác IMC(g.c.g)
=>CK=CM(2 cạnh t/ư)
Lại có: BK+KC=BC
mÀ BN=BK;CK=CM
=>BN+MC=BC(đpcm)
27 tháng 7 2023
a: góc C=180-80-60=40 độ
góc A>góc B>góc C
=>BC>AC>AB
b: Xét ΔBAD và ΔBMD có
BA=BM
góc ABD=góc MBD
BD chung
=>ΔBAD=ΔBMD
c: Xét ΔDAH và ΔDMC có
góc DAH=góc DMC
DA=DM
góc ADH=góc MDC
=>ΔDAH=ΔDMC
=>DH=DC
A B C E F 1 2 1 2 K I
Giải:
Gọi K là giao điểm giữa CF và BE
Kẻ tia phân giác KI của \(\widehat{BKC}\)
\(\Rightarrow\widehat{BKI}=\widehat{CKI}\)
Trong \(\Delta ABC\) có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
\(\Rightarrow60^o+\widehat{B}+\widehat{C}=180^o\)
\(\Rightarrow\widehat{B}+\widehat{C}=120^o\)
\(\Rightarrow\frac{1}{2}\left(\widehat{B}+\widehat{C}\right)=\frac{1}{2}.120^o\)
\(\Rightarrow\frac{1}{2}\widehat{B}+\frac{1}{2}\widehat{C}=60^o\)
\(\Rightarrow\widehat{B_2}+\widehat{C_1}=60^o\)
Xét \(\Delta BKC\) có: \(\widehat{BKC}+\widehat{B_2}+\widehat{C_1}=180^o\)
\(\Rightarrow\widehat{BKC}+60^o=180^o\)
\(\Rightarrow\widehat{BKC}=120^o\)
Ta có: \(\widehat{B_2}+\widehat{C_1}=\widehat{FKB}\)
\(\Rightarrow\widehat{FKB}=60^o\)
Mà \(\widehat{FKB}=\widehat{EKC}\) ( đối đỉnh )
\(\Rightarrow\widehat{EKC}=60^o\)
Xét \(\Delta FKB,\Delta IKB\) có:
\(\widehat{B_1}=\widehat{B_2}\left(=\frac{1}{2}\widehat{B}\right)\)
BK: cạnh chung
\(\widehat{FKB}=\widehat{IKB}\left(=60^o\right)\)
\(\Rightarrow\Delta FKB=\Delta IKB\left(g-c-g\right)\)
\(\Rightarrow BF=BI\) ( cạnh t/ứng )
Xét \(\Delta EKC,\Delta IKC\) có:
\(\widehat{C_1}=\widehat{C_2}\left(=\frac{1}{2}\widehat{C}\right)\)
KC: cạnh chung
\(\widehat{EKC}=\widehat{IKC}\left(=60^o\right)\)
\(\Rightarrow EC=IC\) ( cạnh t/ứng )
Có: \(BI+IC=BC\)
\(\Rightarrow BF+CE=BC\)
\(\Rightarrowđpcm\)