Cho tam giác DEF, I là trung điểm cua EF. Từ E và F kẻ EH⊥DI tại H; FK⊥DI tại K.
a) Chứng minh: IH=IK.
b) Chứng minh: DE+DF>DH+DK.
c) Chứng minh: DH+DK=2DI.
d) Chứng minh: DE+DF>2DI.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 6 2023
a: ED<EF
=>HD<HF
b: Xét ΔDEI có DE=DI và góc D=60 độ
nên ΔDEI đều
c: Xét tứ giác FEBD có
A là trung điểm chung của FB và ED
=>FEBD là hbh
=>FE//BD
=>BD vuông góc DE
31 tháng 1
a: Xét ΔEHD và ΔEHF có
EH chung
\(\widehat{HED}=\widehat{HEF}\)
ED=EF
Do đó: ΔEHD=ΔEHF
c: Ta có; ΔEHD=ΔEHF
=>HF=HD
mà H nằm giữa D và F
nên H là trung điểm của DF
=>\(HD=\dfrac{DF}{2}=3\left(cm\right)\)
ΔEHD vuông tại H
=>\(EH^2+HD^2=ED^2\)
=>\(EH^2=5^2-3^2=16\)
=>\(EH=\sqrt{16}=4\left(cm\right)\)
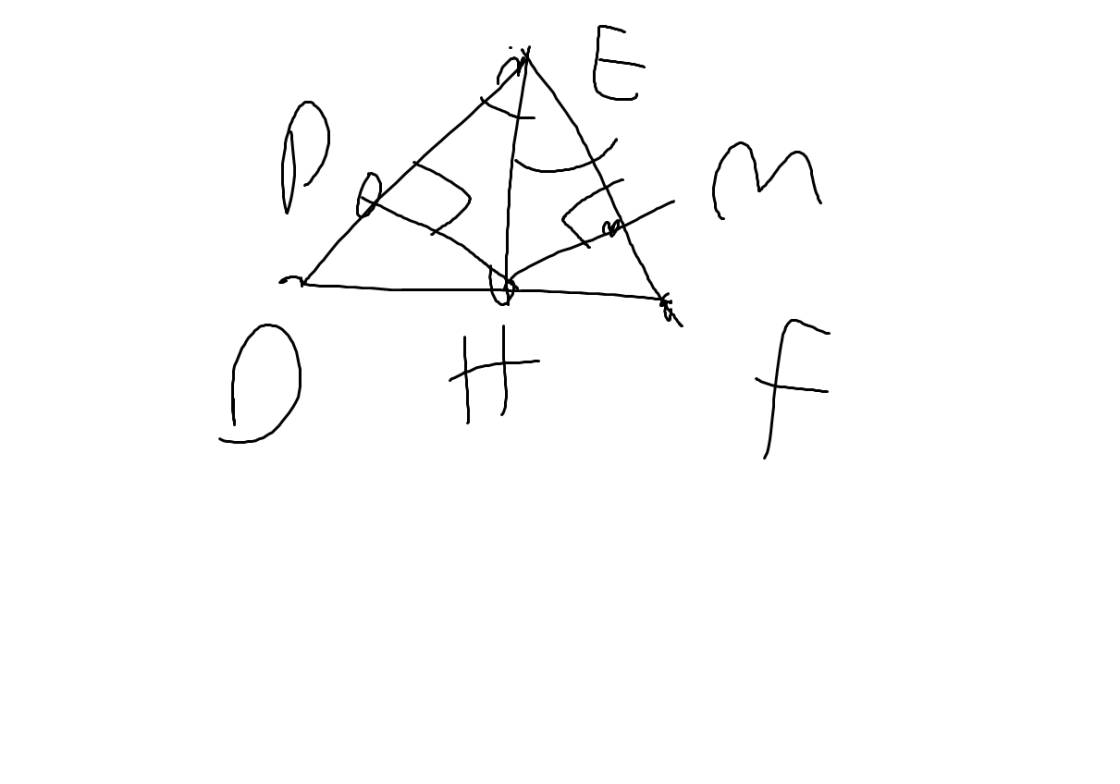
a)xét ΔEHI và ΔFKI có :
\(\widehat{K}=\widehat{H}\)(=90o)
\(\widehat{KIF}=\widehat{EIH}\)(2 góc đối đỉnh)
EI=FI(I là trung điểm của EF)
⇒ΔEHI=ΔFKI(cạnh huyền góc nhọn)
⇒IH=IK(2 cạnh tương ứng)
b)vì ΔEHD vuông tại H
⇒ED > HD (trong tam giác vuông cạnh huyền luôn là cạnh lớn nhất)(1)
chứng minh tương tự với Δ KID
⇒FD > DK (2)
từ (1) và (2) ⇒DE+DF>DH+DK