cho tam giác ABC vuông tại A. Gọi BM là tia phân giác của góc ABC(M thuộc AC). Trên tia BC lấy điểm H sao cho BA=BH.
a; C/M tam giác ABM=HBM
b; C/M Mh vuông BC
c; tia BA cắt tia HM tại K. C/M tam giác KMC cân tại M
d; C/M AH//KC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:
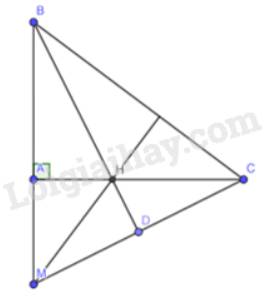
Gọi D giao điểm của tia phân giác của góc B và MC
Xét tam giác BDM và tam giác BDC có :
BD chung
\(\widehat {MBD} = \widehat {CBD}\) ( BD là phân giác của góc B)
BM = BC ( giả thiết )
( \Rightarrow \Delta BDM=\Delta BDC\)(c.g.c)
\( \Rightarrow \widehat {BDM} = \widehat {BDC}\)(2 góc tương ứng)
Mà 2 góc ở vị trí kề bù \( \Rightarrow \widehat {BDM} = \widehat {BDC} = {90^o} \Rightarrow BD \bot CM\)
Mà AC cắt BD tại H \( \Rightarrow \) H là trực tâm tam giác BMC
\( \Rightarrow \) MH là đường cao của tam giác BMC (định lí 3 đường cao đi qua trực tâm tam giác)
\( \Rightarrow \) MH vuông góc với BC

a: Xét ΔABD và ΔHBD có
BA=BH
góc ABD=góc HBD
BD chung
=>ΔABD=ΔHBD
b: Sửa đề: DK=DC
ΔABD=ΔHBD
=>góc BAD=góc BHD=90 độ
=>DH vuông góc BC
Xét ΔDAK vuông tại A và ΔDHC vuông tại H có
DA=DH
góc ADK=góc HDC
=>ΔDAK=ΔDHC
=>AK=HC và DK=DC
c: BA+AK=BK
BH+HC=BC
mà BA=BH và AK=HC
nên BK=BC
BK=BC
DK=DC
=>BD là trung trực của KC
=>B,D,I thẳng hàng

a) Ta có: ΔABC vuông tại A(gt)
nên \(\widehat{ABC}+\widehat{ACB}=90^0\)(hai góc nhọn phụ nhau)
\(\Leftrightarrow\widehat{ACB}=90^0-\widehat{ABC}\)
\(\Leftrightarrow\widehat{ACB}=90^0-60^0\)
hay \(\widehat{ACB}=30^0\)
Vậy: \(\widehat{ACB}=30^0\)
b) Xét ΔADB và ΔEDB có
BA=BE(gt)
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
BD chung
Do đó: ΔADB=ΔEDB(c-g-c)
nên \(\widehat{BAD}=\widehat{BED}\)(hai góc tương ứng)
mà \(\widehat{BAD}=90^0\)(ΔABC vuông tại A)
nên \(\widehat{BED}=90^0\)
hay DE\(\perp\)BC(đpcm)
c) Ta có: BE+EC=BC(E nằm giữa B và C)
BA+AM=BM(A nằm giữa B và M)
mà BE=BA(ΔBED=ΔBAD)
và BC=BM(gt)
nên EC=AM
Xét ΔADM vuông tại A và ΔEDC vuông tại E có
DA=DE(ΔDAB=ΔDEB)
AM=EC(cmt)
Do đó: ΔADM=ΔEDC(hai cạnh góc vuông)
nên \(\widehat{ADM}=\widehat{EDC}\)(hai góc tương ứng)
mà \(\widehat{EDC}+\widehat{ADE}=180^0\)(hai góc kề bù)
nên \(\widehat{ADM}+\widehat{ADE}=180^0\)
\(\Leftrightarrow\widehat{EDM}=180^0\)
hay E,D,M thẳng hàng(đpcm)

ΔBMC cân tại B
mà BH là phân giác
nên BH vuông góc MC
Xét ΔBMC có
CA,BH là đường cao
CA cắt BH tại H
=>H là trực tâm
=>MH vuông góc BC

a: Xét ΔBAM và ΔBNM có
BA=BN
\(\widehat{ABM}=\widehat{NBM}\)
BM chung
Do đó: ΔBAM=ΔBNM
b: Ta có: ΔBAM=ΔBNM
=>MA=MN
=>M nằm trên đường trung trực của AN(1)
ta có: BA=BN
=>B nằm trên đường trung trực của AN(2)
Từ (1) và (2) suy ra BM là đường trung trực của AN
=>BM\(\perp\)AN tại H và H là trung điểm của AN
vì H là trung điểm của AN
nên HA=HN
c: Ta có: CK\(\perp\)BM
HN\(\perp\)BM
Do đó: CK//HN

a: Xét ΔABI vuông tại A và ΔHBI vuông tại H có
BI chung
\(\widehat{ABI}=\widehat{HBI}\)
Do đó:ΔABI=ΔHBI
b: Xét ΔAIK vuông tại A và ΔHIC vuông tại H có
IA=IH
\(\widehat{AIK}=\widehat{HIC}\)
Do đó; ΔAIK=ΔHIC
Suy ra: AK=HC
mà BA=BH
nên BK=BC
=>ΔBKC cân tại B