Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét t/giác ABM và t/giác HBM
có AB = BH (gt)
\(\widehat{ABM}=\widehat{HBM}\)(gt)
BM : chung
=> t/giác ABM = t/giác HBM (c.g.c)
b) Do t/giác ABM = t/giác HBM (cmt)
=> \(\widehat{BAM}=\widehat{BHM}=90^0\) (2 góc t/ứng)
=> HM \(\perp\)BC
c) Xét t/giác AMK và t/giác HMC
có \(\widehat{KAM}=\widehat{MHC}=90^0\)
AM = MJ (do t/giác ABM = t/giác HBM)
\(\widehat{AMK}=\widehat{HMC}\)(đối đỉnh)
=> t/giác ẠMK = t/giác HMC (g.c.g)
=> MK = MC (2 cạnh t/ứng)
=> t/giác KMC cân tại M
c) Ta có: BA + AK = BK
BH + HC = BC
mà AB = BH (gt); AK = HC(do t/giác ABM = t/giác HBM)
=> BK = BC => t/giác BKC cân tại B
=> \(\widehat{K}=\widehat{C}=\frac{180^0-\widehat{B}}{2}\) (2)
Ta có: AB = BH(gt) => t/giác BAH cân tại B
=> \(\widehat{BAH}=\widehat{BHA}=\frac{180^0-\widehat{B}}{2}\)(1)
Từ (1) và (2) => \(\widehat{K}=\widehat{BAH}\)
Mà 2 góc ở vị trí đồng vị => AH // KC

Tự vẽ hình nhé !
a) Xét tam giác ABM và tam giác HBM có:
\(\hept{\begin{cases}BA=BM\left(gt\right)\\BM:chung\\gocB1=gocB2\left(gt\right)\end{cases}}\)
=> tam giác ABM = tam giác HBM (c.g.c)
Mấy câu sau N ở đâu?

ok, thanks nhưng dừng khoảng chừng là 2 giây, you lấy từ qanda

a: Xét ΔBAM và ΔBNM có
BA=BN
\(\widehat{ABM}=\widehat{NBM}\)
BM chung
Do đó: ΔBAM=ΔBNM
b: Ta có: ΔBAM=ΔBNM
=>MA=MN
=>M nằm trên đường trung trực của AN(1)
ta có: BA=BN
=>B nằm trên đường trung trực của AN(2)
Từ (1) và (2) suy ra BM là đường trung trực của AN
=>BM\(\perp\)AN tại H và H là trung điểm của AN
vì H là trung điểm của AN
nên HA=HN
c: Ta có: CK\(\perp\)BM
HN\(\perp\)BM
Do đó: CK//HN

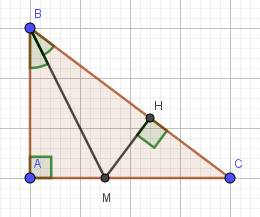
a) Xét hai tam giác vuông: \(\Delta AMB\) và \(\Delta HMB\) có:
BM là cạnh chung
\(\widehat{ABM}=\widehat{HBM}\) (do BM là phân giác của \(\widehat{ABC}\))
\(\Rightarrow\Delta AMB=\Delta HMB\) (cạnh huyền-góc nhọn)
b) Do \(\Delta AMB=\Delta HMB\) (cmt)
\(\Rightarrow AM=HM\) (hai cạnh tương ứng)
c) \(\Delta MHC\) vuông tại H
\(\Rightarrow MC\) là cạnh huyền nên là cạnh lớn nhất
\(\Rightarrow HM< MC\)
Lại có HM = AM (cmt)
\(\Rightarrow AM< MC\)