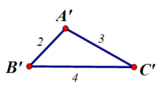
Vẽ thêm tam giác A’B’C’ có :
A’B’ = 2 cm ; B’C’ = 4cm ; A’C’ = 3 cm
Hãy đo rồi so sánh các góc tương ứng của tam giác ABC ở mục 1 và tam giác A’B’C’. Có nhận xét gì về hai tam giác trên ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
1 tháng 7 2019
Ta có thể kết luận được tam giác ABC bằng tam giác A’B’C’ (trường hợp c.g.c)
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
- Độ dài các cạnh tương ứng của 2 tam giác ABC và A’B’C’ bằng nhau.
- Hai tam giác ABC và A'B'C' có bằng nhau.
- Độ dài các cạnh AB' và AC' của hai tam giác em vừa vẽ có bằng các cạnh AB' và AC' của hai tam giác các bạn khác vẽ.
- Hai tam giác em vừa vẽ có bằng hai tam giác mà các bạn khác vẽ.
CM
19 tháng 11 2017
ΔABC và ΔA’B’C’ có:
AB = A’B’
∠B = ∠B'
BC = B’C’
⇒ ΔABC = ΔA’B’C’ (cạnh – góc – cạnh)
HQ
Hà Quang Minh
Giáo viên
17 tháng 9 2023
BC = B’C’ = 6 (ô vuông).
Tam giác ABC và A’B’C’ có các cặp cạnh tương ứng bằng nhau nên tam giác ABC bằng tam giác A’B’C’ (c.c.c)
HQ
Hà Quang Minh
Giáo viên
17 tháng 9 2023
Tam giác ABC có bằng tam giác A’B’C’ (vì 2 tam giác này có thể chồng khít lên nhau).
17 tháng 9 2023
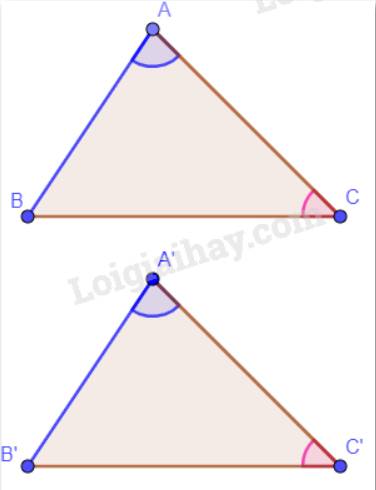
Vì \(\widehat A = \widehat {A'},\widehat C = \widehat {C'}\)mà tổng ba góc trong một tam giác bằng 180° nên \(\widehat B = \widehat {B'}\).
Xét hai tam giác ABC và A’B’C’ có: \(\widehat A = \widehat {A'}\), AB = A’B’, \(\widehat B = \widehat {B'}\).
Vậy \(\Delta ABC = \Delta A'B'C'\)(g.c.g)
Hai tam giác trên có :
∠A = ∠A' ; ∠B = ∠B' ; ∠C = ∠C'
Nhận xét: Hai tam giác trên bằng nhau