Question

[Lạnh Lẽo]

Cho ABC có AB = 3 cm; AC = 4 cm; BC = 5 cm.

a) Chứng tỏ tam giác ABC vuông tại A.

b)Vẽ phân giác BD (D thuộc AC), từ D vẽ DE\(\perp\) BC (E thuộc BC). Chứng minh DA = DE.

c) ED cắt AB tại F. Chứng minh \(\Delta\)ADF = \(\Delta\)EDC rồi suy ra DF > DE.

Answer 1

[Nguyễn Thị Diễm Quỳnh]

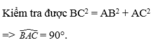
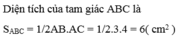
a) Có : \(AB^2+AC^2=3^2+4^2=25\) ; \(BC^2=5^2=25\)

Ta thấy \(AB^2+AC^2=BC^2\Rightarrow\Delta ABC\) vuông tại A

b) Xét \(\Delta ABD\) và \(\Delta EBD\) có:

\(\widehat{BAD}=\widehat{BED}=90^o;BD:chung;\widehat{ABD}=\widehat{EBD}\)

\(\Rightarrow\) \(\Delta ABD\) = \(\Delta EBD\)

\(\Rightarrow\) AD = ED

c) Xét \(\Delta ADF\) và \(\Delta EDC\) có:

\(\widehat{FDA}=\widehat{CDE};AD=ED;\widehat{FAD}=\widehat{CED}=90^o\)

\(\Rightarrow\) \(\Delta ADF\) = \(\Delta EDC\)

\(\Rightarrow\) DF = DC

Xét \(\Delta DEC\) vuông tại E

=> DE < DC mà DC = DF => DE < DF

Answer 2

[Vũ Minh Tuấn]

a) Ta có: AB² + AC² = 3² + 4² = 9 + 16=25

BC² = 5² = 25

=> AB² + AC² = BC² (=25)

Áp dụng định lí Py - ta - go đảo

=> ΔABC vuông tại A.

b) Xét 2 Δ vuông ABD và EBD có:

+) ∠BAD = ∠BED = 90 độ

+) Cạnh BD chung

+) ∠B₁ = ∠B₂ (vì BD là tia phân giác của ∠B)

=> △ABD = ΔEBD (ch - góc nhọn)

=> AD = ED (2 cạnh tương ứng)

c) Xét 2 Δ vuông AFD và ECD có:

+) ∠FAD = ∠CED = 90 độ

+) AD = ED (cmt)

+) ∠FDA = ∠CDE (vì 2 góc đối đỉnh)

=> ΔAFD = ΔECD

=> DF = DC (2 cạnh tương ứng)

Xét △ CED vuông tại E có:

∠CED = 90 độ là góc lớn nhất

=> CD là cạnh lớn nhất

=> CD > ED

mà CD = FD (cmt)

=> FD > ED.

Chúc bạn học tốt!