Chứng minh rằng
a) G=88 + 220 chia hết cho 17
b) H=2+2+22+23+...+260 chia hết cho 3; 7; 15
c) I=E=1+3+32+33+...+31991 chia hết cho 13; 14
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KV
23 tháng 12 2023
A = 8⁸ + 2²⁰
= (2³)⁸ + 2²⁰
= 2²⁴ + 2²⁰
= 2²⁰.(2⁴ + 1)
= 2²⁰.17 ⋮ 17
Vậy A ⋮ 17
19 tháng 7 2021
a) Ta có: \(32^{12}\cdot98^{20}\)
\(=2^{60}\cdot2^{20}\cdot7^{40}\)
\(=2^{80}\cdot7^{40}\)
\(=\left(2^2\cdot7\right)^{40}=28^{40}\)(đpcm)
b) Ta có: \(3^{1994}+3^{1993}-3^{1992}\)
\(=3^{1992}\left(3^2+3-1\right)\)
\(=3^{1992}\cdot11⋮11\)
19 tháng 12 2021
\(1,8^8+2^{20}=2^{24}+2^{20}=2^{20}\left(2^4+1\right)=2^{20}\cdot17⋮17\)
\(2,A=\left(2+2^2\right)+\left(2^3+2^4\right)+...+\left(2^{119}+2^{120}\right)\\ A=2\left(1+2\right)+2^3\left(1+2\right)+...+2^{119}\left(1+2\right)\\ A=3\left(2+2^3+...+2^{119}\right)⋮3\)
\(A=\left(2+2^2+2^3\right)+...+\left(2^{118}+2^{119}+2^{120}\right)\\ A=2\left(1+2+2^2\right)+...+2^{118}\left(1+2+2^2\right)\\ A=\left(1+2+2^2\right)\left(2+...+2^{118}\right)=7\left(2+...+2^{118}\right)⋮7\\ A=\left(2+2^2+2^3+2^4\right)+...+\left(2^{117}+2^{118}+2^{119}+2^{120}\right)\\ A=2\left(1+2+2^2+2^3\right)+...+2^{117}\left(1+2+2^2+2^3\right)\\ A=\left(1+2+2^2+2^3\right)\left(2+...+2^{117}\right)=15\left(2+...+2^{117}\right)⋮15\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
1 tháng 9 2023
Bài 1
a, cm : A = 165 + 215 ⋮ 3
A = 165 + 215
A = (24)5 + 215
A = 220 + 215
A = 215.(25 + 1)
A = 215. 33 ⋮ 3 (đpcm)
b,cm : B = 88 + 220 ⋮ 17
B = (23)8 + 220
B = 216 + 220
B = 216.(1 + 24)
B = 216. 17 ⋮ 17 (đpcm)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
1 tháng 9 2023
c, cm: C = 1 - 2 + 22 - 23 + 24 - 25 + 26 -...-22021 + 22022 : 6 dư 1
C=1+(-2+22-23+24- 25+26)+...+(-22017+22018-22019+22020-22021+22022)
C = 1 + 42 +...+ 22016.(-2 + 22 - 23 + 24 - 25 + 26)
C = 1 + 42+...+ 22016.42
C = 1 + 42.(20+...+22016)
42 ⋮ 6 ⇒ C = 1 + 42.(20+...+22016) : 6 dư 1 đpcm
CM
7 tháng 7 2019
a) A chia hết cho 2 vì tất cả các số hạng của tổng đều chia hết cho 2.
b) Ta tách ghép các số hạng của A thành các nhóm sao cho mỗi nhóm xuất hiện thừa số chia hết cho 3. Khi đó:
10 tháng 10 2021
4₁ A= 2 +2²³ +2 ² + + 220
a₁ A = 2₁ [1 + 2 +2²¹ +. +2¹2):2 Vay A chia hết choi
b₁ A = 2 + 2² +2²+ + 220 (2 +2²) + (2 ² + 2 9) + . + (219+220)
= 2₁ (1 + 2) + 2² (2+1). .. +2 19 (2+1) + = 2₁3 + 2³.3 + ..+ 219.3.
= (2+2 ³+ + 219) 3:3 Vậy A chia hết cho 3 A = 2 + 2 ² + 2³ + 2ª +. 20 + 2.9+ +2
2+2 ³ + 2² +2²4 + + 218 + 720 +2²³ +2²+ +218 +220 2. (2 +2²) + 2² (1+2²) +.. + 218 ( 1 +2²) = 2 5 +2²5 + + 218 5. 12 +2° + 2 ... +218 ) 5 : 5.
vậy A chia hết cho 5
PT
1
PT
1
CM
24 tháng 4 2019
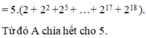
Sơ đồ con đường |
Lời giải chi tiết |
|
Ta có: C = 2 + 2 2 + 2 3 + 2 4 + ... + 2 59 + 2 60 = 2 1 + 2 + 2 3 1 + 2 + ... + 2 59 1 + 2 = 2.3 + 2 3 .3 + ... + 2 59 .3 = 2 + 2 3 + ... + 2 59 .3 ⇒ C ⋮ 3 |
OY
21 tháng 8 2021
b) A=2+22+23+...+220
A=(2+22)+(23+24)+...+(219+220)
A=3.2+3.23+...+3.219
A=3.(2+23+25+...+219)
⇒A⋮3
phần c) làm tương tự
NG
1
H9
HT.Phong (9A5)
CTVHS
17 tháng 10 2023
a) \(A=2+2^2+2^3+...+2^{20}\)
\(A=\left(2+2^2\right)+\left(2^3+2^4\right)+...+\left(2^{19}+2^{20}\right)\)
\(A=2\cdot\left(1+3\right)+2^3\cdot\left(1+3\right)+...+2^{59}\cdot\left(1+3\right)\)
\(A=3\cdot\left(2+2^3+...+2^{59}\right)\)
Vậy A chia hết cho 3
________
\(A=2+2^2+2^3+...+2^{20}\)
\(A=\left(2+2^3\right)+\left(2^2+2^4\right)+...+\left(2^{58}+2^{60}\right)\)
\(A=2\cdot\left(1+4\right)+2^2\cdot\left(1+4\right)+...+2^{58}\cdot\left(1+4\right)\)
\(A=5\cdot\left(2+2^2+...+2^{58}\right)\)
Vậy A chia hết cho 5
a: \(G=8^8+2^{20}\)
\(=2^{24}+2^{20}\)
\(=2^{20}\left(2^4+1\right)=2^{20}\cdot17⋮17\)
b: Sửa đề: \(H=2+2^2+2^3+...+2^{60}\)
\(=2\left(1+2\right)+2^3\left(1+2\right)+...+2^{59}\left(1+2\right)\)
\(=3\left(2+2^3+...+2^{59}\right)⋮3\)
\(H=2+2^2+2^3+...+2^{60}\)
\(=2\left(1+2+2^2\right)+2^4\left(1+2+2^2\right)+...+2^{58}\left(1+2+2^2\right)\)
\(=7\left(2+2^4+...+2^{58}\right)⋮7\)
\(H=2+2^2+2^3+...+2^{60}\)
\(=\left(2+2^2+2^3+2^4\right)+...+\left(2^{57}+2^{58}+2^{59}+2^{60}\right)\)
\(=2\left(1+2+2^2+2^3\right)+...+2^{57}\left(1+2+2^2+2^3\right)\)
\(=15\left(2+2^5+...+2^{57}\right)⋮15\)
c: \(E=\left(1+3+3^2\right)+3^3\left(1+3+3^2\right)+...+3^{1989}\left(1+3+3^2\right)\)
\(=13\left(1+3^3+...+3^{1989}\right)⋮13\)
\(E=1+3+3^2+3^3+...+3^{1991}\)
\(=\left(1+3+3^2+3^3+3^4+3^5\right)+\left(3^6+3^7+3^8+3^9+3^{10}+3^{11}\right)+...+3^{1986}+3^{1987}+3^{1988}+3^{1989}+3^{1990}+3^{1991}\)
\(=364\left(1+3^6+...+3^{1986}\right)⋮14\)