Cho góc b với 0 ◦ ≤ b ≤ 180◦ có điểm biểu diễn là B(0; 1). Khẳng định nào sau đây đúng? A. b = 10◦ . B. b = 90◦ . C. b = 0 ◦ . D. b = 180◦ .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
27 tháng 2 2017
a. Điểm biểu diễn các số: - 2; - 3; - 1 đều đặt ở bên trái điểm 0 nên các số này đều nhỏ hơn số 0;
Điểm biểu diễn các số 1; 2; 4 đều đặt ở bên phải điểm 0 nên các số này đều lớn hơn số 0.
b. Điểm – 2 và 2 nằm về hai phía của điểm 0 và cách đều điểm 0.
c. Chỉ đúng với trường hợp những điểm nằm về bên phải điểm 0. Đối với những điểm nằm về bên trái điểm 0 thì ngược lại: điểm nào ở xa gốc hơn thì biểu diễn số nhỏ hơn.
28 tháng 11 2014
Tự vẽ hình nhé
a) Trong tam giác ABC có Â + góc B + góc C = 1800 ( định lí )
=> 1800 - Â = góc B + góc C
Ta có Â = 1800 - 3.góc C
=> 1800 - Â = 3.góc C
=> góc B + góc C = 3. góc C
=> góc B = 3.góc C - góc C
=> góc B = 2. góc C
c) Xin lỗi mình ko biết làm
T
11 tháng 8 2017
a) Trong tam giác ABC có \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
\(\Rightarrow180^o-\widehat{A}=\widehat{B}+\widehat{C}\)
Ta có \(\widehat{A}=180^o-3.\widehat{C}\)
\(\Rightarrow180^o-\widehat{A}=3.\widehat{C}\)
\(\Rightarrow\widehat{B}+\widehat{C}=3.\widehat{C}\)
\(\Rightarrow\widehat{B}=3.\widehat{C}-\widehat{C}\)
Tự làm tiếp
b) Vẽ hình ra!
c) Xin lỗi! Mình không biết
CM
19 tháng 12 2018
Đáp án C
Phương pháp.
Tính trực tiếp 
Lời giải chi tiết.
Ta có
Do 
Do đó M có phần thực âm, phần ảo bằng 0, nên thuộc tia đối của tia Ox.
21 tháng 9 2023
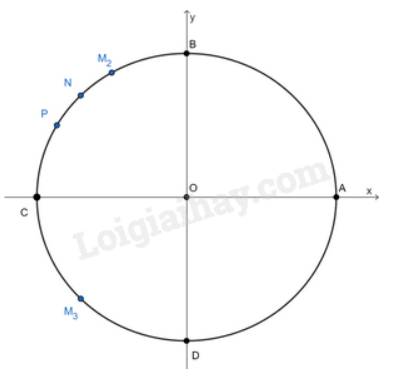
a) Ta có: \(\frac{{\frac{{2\pi }}{3}}}{{2\pi }} = \frac{1}{3}\). Ta chia đường tròn thành 3 phần bằng nhau. Khi đó điểm \({M_2}\) là điểm biểu diễn bởi góc có số đo \(\frac{{2\pi }}{3}\).
b) Ta có \( - \frac{{11\pi }}{4} = - \frac{{3\pi }}{4} + \left( { - 1} \right).2\pi \). Do đó điểm biểu diễn bởi góc \( - \frac{{11\pi }}{4}\) trùng với góc \( - \frac{{3\pi }}{4}\) và là điểm \({M_3}\).
c) Ta có \(\frac{{150}}{{180}} = \frac{5}{6}\). Ta chia nửa đường tròn thành 6 phần bằng nhau. Khi đó P là điểm biểu diễn bởi góc \({150^0}\)
d) Ta có \( - {225^0} = - {180^0} - {45^0}\). Do đó điểm biểu diễn N là điểm biểu diễn bởi góc \( - {225^0}\)
