Lập phương trình của mặt phẳng ( α ) đi qua điểm M(3; -1; -5) đồng thời vuông góc với hai mặt phẳng:
( β ): 3x – 2y + 2z + 7 = 0
( γ ): 5x – 4y + 3z + 1 = 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
25 tháng 8 2019
Mặt phẳng ( α ) đi qua hai điểm A, B và vuông góc với mặt phẳng ( β ): x + 2y – z = 0.
Vậy hai vecto có giá song song hoặc nằm trên ( α ) là AB → = (2; 2; 1) và n β → = (1; 2; −1).
Suy ra ( α ) có vecto pháp tuyến là: n α → = (−4; 3; 2)
Vậy phương trình của ( α ) là: -4x + 3(y – 1) + 2z = 0 hay 4x – 3y – 2z + 3 = 0
CM
10 tháng 1 2018
Gọi giao điểm của (α) với ba tia Ox, Oy, Oz lần lượt là A(a; 0; 0), B(0; b; 0), C(0; 0 ; c) (a, b, c > 0).
Mặt phẳng (α) có phương trình theo đoạn chắn là:
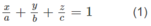
Do (α) đi qua M(1; 2; 3) nên ta thay tọa độ của điểm M vào (1):
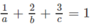
Thể tích của tứ diện OABC là:
Áp dụng bất đẳng thức Cô-si ta có:
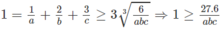
⇒ abc ≥ 27.6 ⇒ V ≥ 27
Ta có: V đạt giá trị nhỏ nhất ⇔ V = 27
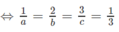
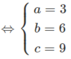
Vậy phương trình mặt phẳng ( α ) thỏa mãn đề bài là:
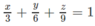
hay 6x + 3y + 2z – 18 = 0
CM
12 tháng 4 2017
Đáp án C
Phương trình mặt phẳng qua M và song song với ( α ) là:
3(x-3)-(y+1)+2(z+2)=0 ⇔ 3x-y+2z-6=0
CM
1 tháng 10 2019
Đáp án B.
Phương pháp: Mặt phẳng ( α ) đi qua M(1; –3;4) và nhận n ( β ) → = ( 6 ; 2 - 1 ) là 1 VTPT.
Cách giải: Mặt phẳng ( α ) đi qua M(1; –3;4) và nhận n ( β ) → = ( 6 ; 2 - 1 ) là 1 VTPT nên có phương trình:
6(x– 1) + 2(y+3) – (z– 4) = 0 → 6x + 2y – z +4 = 0
CM
2 tháng 1 2020
Đáp án A
Phương trình mặt phẳng (α): 2(x - 1) + 3(y + 2) + 5(z - 4)=0<=> 2x + 3y + 5z - 16=0.
Mặt phẳng ( α ) vuông góc với hai mặt phẳng ( β ) và ( γ ), do đó hai vecto có giá song song hoặc nằm trên ( α ) là: n β → = (3; −2; 2) và n γ → = (5; −4; 3).
Suy ra n α → = n β → ∧ n γ → = (2; 1; −2)
Mặt khác ( α )( α ) đi qua điểm M(3; -1; -5) và có vecto pháp tuyến là n α → . Vậy phương trình của ( α ) là: 2(x – 3) + 1(y + 1) – 2(z + 5) = 0 hay 2x + y – 2z – 15 = 0.