cho tam giác abc vuông tại a , kẻ ah vuông góc với bc tại h . Trên tia đối của tia ah lấy điểm d sao cho hd=ha
Chứng minh
a; ∆ABH=∆DBH
b; BD vuông góc với DC
c; CB là tia phân giác của góc ACD
Cứu mị với bất lực quá
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
16 tháng 2 2019
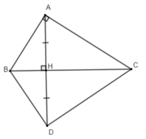
Ta có D thuộc tia đối của tia HA nên H nằm giữa hai điểm A và D
Mà HA = HD nên H là trung điểm của AD
Mặt khác B C ⊥ A D tại H (do A H ⊥ B C )
Do đó BC là đường trung trực của đoạn thẳng AD
Suy ra B A = B D C A = C D (tính chất điểm nằm trên đường trung trực của đoạn thẳng)
Xét tam giác ABC và tam giác DBC có:
BA = BD; CA = CD (cmt)
BC cạnh chung
Do đó: Δ A B C = Δ D B C (c – c – c)
Suy ra B D C ^ = B A C ^ = 90 ° (hai góc tương ứng)
Vậy tam giác BDC vuông tại D.
Chọn đáp án C
31 tháng 7 2021
a) Xét ΔAHB vuông tại H và ΔDHB vuông tại H có
BH chung
AH=DH(gt)
Do đó: ΔAHB=ΔDHB(hai cạnh góc vuông)
13 tháng 4 2021
a)
Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC(ΔABC cân tại A)
AH chung
Do đó: ΔABH=ΔACH(cạnh huyền-cạnh góc vuông)
Suy ra: BH=CH(hai cạnh tương ứng)
Xét ΔABH vuông tại H và ΔDCH vuông tại D có
AH=DH(gt)
BH=CH(cmt)
Do đó: ΔABH=ΔDCH(hai cạnh góc vuông)
Suy ra: AB=DC(Hai cạnh tương ứng)
mà AB=AC(ΔABC cân tại A)
nên AC=DC(đpcm)
13 tháng 4 2021
b) Xét ΔAHE vuông tại H và ΔDHE vuông tại H có
EH chung
AH=DH(gt)
Do đó: ΔAHE=ΔDHE(hai cạnh góc vuông)
Suy ra: AE=DE(Hai cạnh tương ứng)
Xét ΔACE và ΔDCE có
CA=CD(cmt)
CE chung
AE=DE(cmt)
Do đó: ΔACE=ΔDCE(c-c-c)
24 tháng 3 2020
Câu hỏi của Nguyễn Hiếu Nhân - Toán lớp 7 - Học toán với OnlineMath
a: Xét ΔABH vuông tại H và ΔDBH vuông tại H có
BH chung
HA=HD
Do đó: ΔABH=ΔDBH
b: Xét ΔABC và ΔDBC có
BA=BD
góc ABC=góc DBC
BC chung
Do đó: ΔABC=ΔDBC
=>góc BDC=90 độ
c: ΔABC=ΔDBC
nên góc ACB=góc DCB
=>CB là phân giác của góc ACD