Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

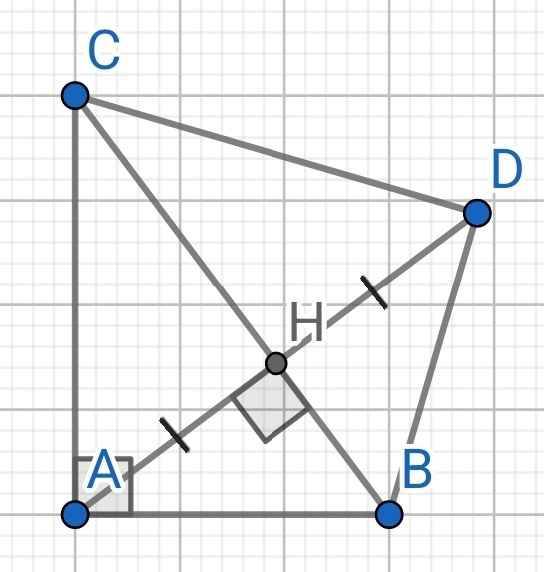 a) Xét hai tam giác vuông: ∆ABH và ∆DBH có:
a) Xét hai tam giác vuông: ∆ABH và ∆DBH có:
AH = DH (gt)
BH là cạnh chung
⇒ ∆ABH = ∆DBH (hai cạnh góc vuông)
b) Sửa đề: Chứng minh ∠BDC = 90⁰
Do ∆ABH = ∆DBH (cmt)
⇒ ∠ABH = ∠DBH (hai góc tương ứng)
AB = BD (hai cạnh tương ứng)
Do ∠ABH = ∠DBH (cmt)
⇒ ∠ABC = ∠DBC
Xét ∆ABC và ∆DBC có:
AB = BD (cmt)
∠ABC = ∠DBC (cmt)
BC là cạnh chung
⇒ ∆ABC = ∆DBC (c-g-c)
⇒ ∠BAC = ∠BDC = 90⁰
Vậy ∠BDC = 90⁰

a) Chứng minh được tam giác ABC = tam giác A.BD (c-g-c), từ đó suy ra được tam giác BCD đều
b) Dùng kết quả câu a, ta có BC = CD = 2AC

a)Xet 2 tam giac vuong AHB va DHC co:
HC chung
DH = AH
=>\(\Delta\)AHB = \(\Delta\)AHC (2 canh goc vuong)
Ta co : CA=CD (2 canh tuong ung)
=>\(\Delta\)CAD can
b)

a,xét tam giác ACH và tam giác DCH có:
HA=HD(gt)
góc CHA= góc CHD(vì CH\(\perp\)AD)
HC chung => tam giác ACH=tam giác DCH(c.g.c)
tam giác ADC có CH vừa là trung tuyến đồng thời là đường cao=>tam giác ADC cân tại C
b,xét tam giác AHB và tam giác DHE có:
góc BHA= góc DHE( đối đỉnh)
HA=HD(cmt), HB=HE(gT)=>tam giác AHB= tam giác DHE(c.g.c)
gọi giao điểm DE với AC là K
vì tam giác AHB= tam giác DHE(cmt)=>góc HED= góc HBA
mà góc HED=góc CEK( đối đỉnh)=> góc HBA=góc CEK
lại có tam giác ABC vuông tại A=> góc HBA+ góc ECK=90 độ=> góc CEK+góc ECK=90 độ=>DK\(\perp AC\)
hay DE \(\perp AC\) mà CE\(\perp AD\)(tại H)=>E là trực tâm tam giác ADC
ăn cơm đã ý c tí mik làm sau

a: \(BC=\sqrt{34}\left(cm\right)\)
b: Xét ΔBCD có
CA là đường cao
CA là đường trung tuyến
Do đó:ΔCBD cân tại C
c: Xét ΔCKA vuông tại K và ΔCHA vuông tại H có
CA chung
\(\widehat{KCA}=\widehat{HCA}\)
Do đó: ΔCKA=ΔCHA
Suy ra: CK=CH
d: Xét ΔCBD có CK/CD=CH/CB
nên HK//BD

a) Xét \(\Delta\)AHB và \(\Delta\)DHB có:
^AHB = ^DHB ( 1v )
HA = HD ( giả thiết )
MH chung
=> \(\Delta\)AHB = \(\Delta\)DHB ( c.g.c)
b) Từ (a) => ^ABH = ^DHB => BH là phân giác ^ABD
Vì \(\Delta\)ABC nhọn => H nằm trong đoạn BC
=> BC là phân giác ^ABD
c) NF vuông BC
AH vuông BC
=> NF // AH
=> ^NFM = ^HAM ( So le trong )
Lại có: ^HMA = NMF ( đối đỉnh ) và MA = MF ( giả thiết )
=> \(\Delta\)NFM = \(\Delta\)HAM ( g.c.g)
=> NF = AH ( 2)
Từ ( a) => AH = HD ( 3)
Từ (2) ; (3) => NF = HD

a: Xét ΔBCD vuông tại C và ΔBMD vuông tại M có
BD chung
\(\widehat{CBD}=\widehat{MBD}\)
Do đó: ΔBCD=ΔBMD
b: Ta có: ΔBCD=ΔBMD
=>BC=BM và DC=DM
Xét ΔBCM có BC=BM và \(\widehat{CBM}=60^0\)
nên ΔBCM đều
Ta có: BD là phân giác của góc CBA
=>\(\widehat{CBD}=\widehat{DBA}=\dfrac{\widehat{CBA}}{2}=\dfrac{60^0}{2}=30^0\)
Ta có: ΔBCA vuông tại C
=>\(\widehat{CBA}+\widehat{CAB}=90^0\)
=>\(\widehat{CAB}=90^0-60^0=30^0\)
Xét ΔDBA có \(\widehat{DAB}=\widehat{DBA}\left(=30^0\right)\)
nên ΔDAB cân tại D
c: Xét ΔDCK vuông tại C và ΔDMA vuông tại M có
DC=DM
CK=MA
Do đó: ΔDCK=ΔDMA
=>DK=DA
=>ΔDKA cân tại D
Ta có: BC+CK=BK
BM+MA=BA
mà BC=BM và CK=MA
nên BK=BA
=>ΔBKA cân tại B

Ta có D thuộc tia đối của tia HA nên H nằm giữa hai điểm A và D
Mà HA = HD nên H là trung điểm của AD
Mặt khác B C ⊥ A D tại H (do A H ⊥ B C )
Do đó BC là đường trung trực của đoạn thẳng AD
Suy ra B A = B D C A = C D (tính chất điểm nằm trên đường trung trực của đoạn thẳng)
Xét tam giác ABC và tam giác DBC có:
BA = BD; CA = CD (cmt)
BC cạnh chung
Do đó: Δ A B C = Δ D B C (c – c – c)
Suy ra B D C ^ = B A C ^ = 90 ° (hai góc tương ứng)
Vậy tam giác BDC vuông tại D.
Chọn đáp án C