Cho (O) và một điểm M nằm ngoài đường tròn. Qua M kẻ hai đường thẳng, một đường cắt (O) tại A,B; đường còn lại cắt (O) tại C,D. c/m MA.MB=MC.MD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 7 2023
a: góc ACB=1/2*sđ cung AB=90 độ
=>ΔACN vuông cân tại C
góc ACN+góc AMN=180 độ
=>AMNC nội tiếp
b: AMNC nội tiếp
=>góc CNA=góc CMA=góc BMD
góc BNE=1/2(sđ cung BE-sđ cung AC)
góc DMB=1/2*(sđ cung BD-sđ cung AC)
=>sđ cung BD=sđ cung BE
=>B nằm trên trung trực của DE
Xét ΔADB và ΔAEB có
góc ADB=góc aEB
AB chung
DB=BE
=>ΔABD=ΔAEB
=>AD=AE
=>A nằm trên trung trực của DE
=>AB là trung trực của DE
=>DE vuông góc AB
MH
25 tháng 1 2023
Mình làm tắt nha bạn không hiểu đâu thì hỏi lại nhé
a) MA, MB là tiếp tuyến
=> \(\widehat{OBM}=\widehat{OAM}=90^o\) (t/c tiếp tuyến)
=> \(\widehat{OBM}+\widehat{OAM}=180^o\)
mà 2 góc đối nhau
=> tứ giác AOBM nội tiếp
=> 4 điểm A, O, B, M cùng thuộc 1 đường tròn
b) Áp dụng hệ thức lượng vào tam giác OAM vuông tại A đường cao AH
=> \(AM^2=MH.MO\)
Áp dụng hệ thức lượng vào tam giác DAM vuông tại A đường cao AC
=> \(AM^2=MC.MD\)
=> \(AM^2=MH.MO=MC.MD\)
VT
18 tháng 1 2024
Câu a),b) tự làm nhé , mình chỉ giúp câu c) thôi .
OI vuông góc NP ( Do I là trung điểm của MP ) , OF vuông góc NP ( Do OF là đường trung trực của NP )
=> O,I,F thẳng hàng
Tam giác ONF vuông tại N , đường cao NI
=> ON^2 = OI.OF
Mà ON=OA
OA^2 = OH.OM
=> OH.OM=OI.OF
=> OH/OI=OF/OM
Xét tam giác OIM và tam giác OHF có
góc MOF chung
OH/OI=OF/OM
=> Tam giác OIM đồng dạng tam giác OHF
=> góc OHF=góc OIM (=90 độ )
OH vuông HF
mà OH vuông AB
=> A,B,F thẳng hàng
=> F nằm trên đường thẳng cố định AB khi đường thẳng d quay quanh M mà vẫn thỏa mãn các yêu cầu đề bài
Điều phải chứng minh
1 tháng 3 2022
a, Ta có SA = SB (tc tiếp tuyến cắt nhau )
OA = OB = R
Vậy OS là đường trung trực đoạn AB
=> SO vuông AB tại H
b, Vì I là trung điểm
=> OI vuông NS
Xét tứ giác IHSE ta có ^EHS = ^EIS = 900
mà 2 góc này kề, cùng nhìn cạnh ES
Vậy tứ giác IHSE nt 1 đường tròn
=> ^ESH = ^HIO ( góc ngoài đỉnh I )
Xét tam giác OIH và tam giác OSE có
^HIO = ^OSE (cmt)
^O_ chung
Vậy tam giác OIH ~ tam giác OSE (g.g)
\(\dfrac{OI}{OS}=\dfrac{OH}{OE}\Rightarrow OI.OE=OH.OS\)
Xét tam giác OAS vuông tại A ( do SA là tiếp tuyến với A là tiếp điểm), đường cao AH ta có
\(OA^2=OH.OS\)(hệ thức lượng)
\(\Rightarrow OA^2=R^2=OI.OE\)
CM
8 tháng 1 2017
TH1: M nằm trong đường tròn.
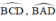là hai góc nội tiếp cùng chắn cung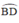 
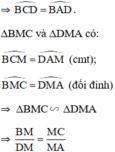
⇒ MA.MB = MC.MD
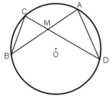
TH2: M nằm ngoài đường tròn.
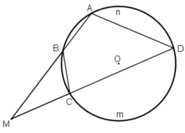
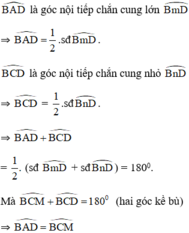
ΔMBC và ΔMDA có:
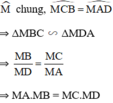
Kiến thức áp dụng
+ Góc nội tiếp chắn một cung có số đo bằng một nửa số đo của cung đó.
+ Hai góc nội tiếp chắn cùng một cung thì có số đo bằng nhau.
CM
18 tháng 7 2018
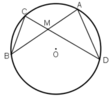
TH1: M nằm trong đường tròn.
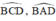là hai góc nội tiếp cùng chắn cung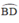 
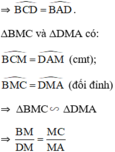
⇒ MA.MB = MC.MD
TH2: M nằm ngoài đường tròn.
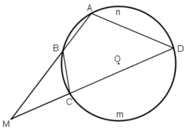
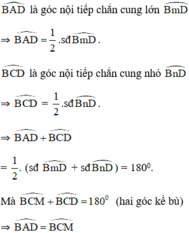
ΔMBC và ΔMDA có:
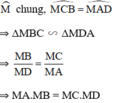
Xét (O) có
\(\widehat{ADC}\) là góc nội tiếp chắn cung AC
\(\widehat{ABC}\) là góc nội tiếp chắn cung AC
Do đó: \(\widehat{ADC}=\widehat{ABC}\)
=>\(\widehat{MDA}=\widehat{MBC}\)
Xét ΔMDA và ΔMBC có
\(\widehat{MDA}=\widehat{MBC}\)
\(\widehat{M}\) chung
Do đó: ΔMDA đồng dạng với ΔMBC
=>\(\dfrac{MD}{MB}=\dfrac{MA}{MC}\)
=>\(MD\cdot MC=MB\cdot MA\)