Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
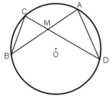
TH1: M nằm trong đường tròn.
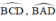là hai góc nội tiếp cùng chắn cung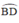 
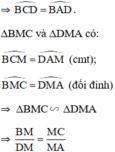
⇒ MA.MB = MC.MD
TH2: M nằm ngoài đường tròn.
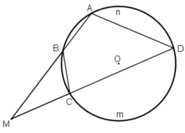
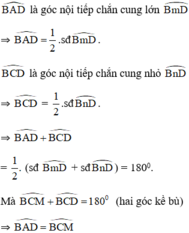
ΔMBC và ΔMDA có:
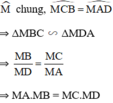
Kiến thức áp dụng
+ Góc nội tiếp chắn một cung có số đo bằng một nửa số đo của cung đó.
+ Hai góc nội tiếp chắn cùng một cung thì có số đo bằng nhau.
a) M ở bên trong đường tròn (hình a)
Xét hai tam giác MAB' và MA'B chúng có:
=
( đối đỉnh)
=
(hai góc nội tiếp cùng chắn cung
).
Do đó ∆MAB' ~ ∆MA'B, suy ra:
=
, do đó MA. MB = MB'. MA'
b) M ở bên ngoài đường tròn (hình b)
∆MAB' ~ ∆MA'B
M chung =
(hai góc nội tiếp cùng chắn cung
).
Suy ra: =
hay MA. MB = MB'. MA'
Xét (O) có
\(\widehat{ADC}\) là góc nội tiếp chắn cung AC
\(\widehat{ABC}\) là góc nội tiếp chắn cung AC
Do đó: \(\widehat{ADC}=\widehat{ABC}\)
=>\(\widehat{MDA}=\widehat{MBC}\)
Xét ΔMDA và ΔMBC có
\(\widehat{MDA}=\widehat{MBC}\)
\(\widehat{M}\) chung
Do đó: ΔMDA đồng dạng với ΔMBC
=>\(\dfrac{MD}{MB}=\dfrac{MA}{MC}\)
=>\(MD\cdot MC=MB\cdot MA\)
a: góc ACB=1/2*sđ cung AB=90 độ
=>ΔACN vuông cân tại C
góc ACN+góc AMN=180 độ
=>AMNC nội tiếp
b: AMNC nội tiếp
=>góc CNA=góc CMA=góc BMD
góc BNE=1/2(sđ cung BE-sđ cung AC)
góc DMB=1/2*(sđ cung BD-sđ cung AC)
=>sđ cung BD=sđ cung BE
=>B nằm trên trung trực của DE
Xét ΔADB và ΔAEB có
góc ADB=góc aEB
AB chung
DB=BE
=>ΔABD=ΔAEB
=>AD=AE
=>A nằm trên trung trực của DE
=>AB là trung trực của DE
=>DE vuông góc AB
Đường tròn c: Đường tròn qua B_1 với tâm O Đoạn thẳng i: Đoạn thẳng [F, A] Đoạn thẳng k: Đoạn thẳng [A, C] Đoạn thẳng l: Đoạn thẳng [A, E] Đoạn thẳng m: Đoạn thẳng [E, M] Đoạn thẳng n: Đoạn thẳng [D, F] Đoạn thẳng p: Đoạn thẳng [G, B] Đoạn thẳng q: Đoạn thẳng [E, C] O = (2.08, 1.84) O = (2.08, 1.84) O = (2.08, 1.84) A = (12.48, 2.58) A = (12.48, 2.58) A = (12.48, 2.58) Điểm B: Điểm trên c Điểm B: Điểm trên c Điểm B: Điểm trên c Điểm D: Điểm trên c Điểm D: Điểm trên c Điểm D: Điểm trên c Điểm C: Giao điểm đường của c, f Điểm C: Giao điểm đường của c, f Điểm C: Giao điểm đường của c, f Điểm E: Giao điểm đường của c, g Điểm E: Giao điểm đường của c, g Điểm E: Giao điểm đường của c, g Điểm F: Giao điểm đường của c, h Điểm F: Giao điểm đường của c, h Điểm F: Giao điểm đường của c, h Điểm G: Giao điểm đường của c, i Điểm G: Giao điểm đường của c, i Điểm G: Giao điểm đường của c, i Điểm M: Giao điểm đường của f, j Điểm M: Giao điểm đường của f, j Điểm M: Giao điểm đường của f, j
a) Do DF // AC nên \(\widehat{MAG}=\widehat{GFD}\) (Hai góc so le trong) .
Lại có \(\widehat{GFD}=\widehat{GED}\) (Hai góc nội tiếp cùng chắn cung GD)
Nên \(\widehat{MAG}=\widehat{GED}\)
Xét tam giác AMG và tam giác EMA có:
\(\widehat{MAG}=\widehat{MEA}\) (cmt)
Góc M chung
Vậy nên \(\Delta AMG\sim\Delta EMA\left(g-g\right)\Rightarrow\frac{MA}{ME}=\frac{MG}{MA}\Rightarrow MA^2=MG.ME\)
b) Do tứ giác ECBG nội tiếp nên \(\widehat{BCE}=\widehat{BGM}\) (Góc ngoài tại đỉnh đối của tứ giác nội tiếp)
Vậy xét tam giác MGB và MCE có:
\(\widehat{BGM}=\widehat{ECM}\left(cmt\right)\)
Góc M chung
Vậy nên \(\Delta MGB\sim\Delta MCE\left(g-g\right)\)
c) Theo câu a, ta có \(AM^2=MG.ME\)
Theo câu b, \(\Delta MGB\sim\Delta MCE\Rightarrow\frac{MG}{MC}=\frac{MB}{ME}\Rightarrow MG.ME=MB.MC\)
Vậy nên \(MA^2=MB.MC\)
Suy ra \(MA^2+MA.MC=MB.MC+MA.MC\)
\(\Leftrightarrow MA\left(MA+MC\right)=MC\left(MB+MA\right)\)
\(\Leftrightarrow MA.AC=MC.AB\)
\(\Leftrightarrow AB\left(AC-AM\right)=MA.AC\)
\(\Leftrightarrow AB.AC-AB.AM=AM.AC\)
\(\Leftrightarrow AB.AC=AM\left(AB+AC\right)\)
\(\Leftrightarrow\frac{1}{AM}=\frac{AB+AC}{AB.AC}\)
\(\Leftrightarrow\frac{1}{AM}=\frac{1}{AB}+\frac{1}{AC}\left(đpcm\right)\)
TH1: M nằm trong đường tròn.
⇒ MA.MB = MC.MD
TH2: M nằm ngoài đường tròn.
ΔMBC và ΔMDA có: