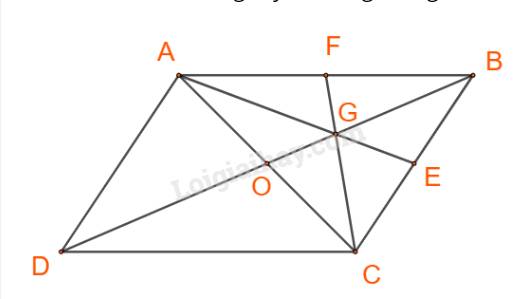
ABCD là hình bình hành, I là trung điểm của CD, G là trọng tâm tam giác BCI, \(\overrightarrow{a}=\overrightarrow{AB};\overrightarrow{b}=\overrightarrow{AD}\). Đẳng thức đúng:
A. \(\overrightarrow{AG}=\frac{5}{6}\overrightarrow{a}+\frac{2}{3}\overrightarrow{b}\)
B. \(\overrightarrow{AG}=\frac{4}{3}\overrightarrow{a}+\frac{2}{3}\overrightarrow{b}\)
C. \(\overrightarrow{AG}=\frac{5}{6}\overrightarrow{a}+\overrightarrow{b}\)
D. \(\overrightarrow{AG}=\overrightarrow{a}+\frac{5}{6}\overrightarrow{b}\)





\(\overrightarrow{BI}=\overrightarrow{BC}+\overrightarrow{CI}=\overrightarrow{BC}-\frac{1}{2}\overrightarrow{AB}\)
\(\overrightarrow{BG}=\frac{1}{3}\left(\overrightarrow{BI}+\overrightarrow{BC}\right)=\frac{1}{3}\left(\overrightarrow{BC}-\frac{1}{2}\overrightarrow{AB}+\overrightarrow{BC}\right)=\frac{2}{3}\overrightarrow{BC}-\frac{1}{6}\overrightarrow{AB}\)
\(\overrightarrow{AG}=\overrightarrow{AB}+\overrightarrow{BG}=\overrightarrow{AB}+\frac{2}{3}\overrightarrow{BC}-\frac{1}{6}\overrightarrow{AB}=\frac{5}{6}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{BC}=\frac{5}{6}\overrightarrow{a}+\frac{2}{3}\overrightarrow{b}\)