Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

TenAnh1
TenAnh1
A = (-4.3, -5.94)
A = (-4.3, -5.94)
A = (-4.3, -5.94)
B = (11.06, -5.94)
B = (11.06, -5.94)
B = (11.06, -5.94)
D = (10.84, -5.94)
D = (10.84, -5.94)
D = (10.84, -5.94)
a)
\(\overrightarrow{AO}=\overrightarrow{AB}+\overrightarrow{BO}=\overrightarrow{AB}+\overrightarrow{AF}\).
Vậy \(\overrightarrow{AD}=2\overrightarrow{AO}=2\left(\overrightarrow{AB}+\overrightarrow{AF}\right)\).
b)
\(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{BC}=\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{BC}\right)=\dfrac{1}{2}\overrightarrow{AC}\).
Vì vậy: \(\left|\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{BC}\right|=\left|\dfrac{1}{2}\overrightarrow{AC}\right|=\dfrac{1}{2}AC\).
A B C a H
Do tam giác ABC cân tại B nên BH là đường cao, đường trung tuyến, đường phân giác ứng với đỉnh B của tam giác ABC.
Áp dụng hệ thức lượng trong tam giác vuông ta có:
\(AH=AB.sin60^o=\dfrac{a\sqrt{3}}{2}\).
\(AC=2BH=2.\dfrac{a\sqrt{3}}{2}=a\sqrt{3}\).
Vì vậy: \(\left|\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{BC}\right|=\left|\dfrac{1}{2}\overrightarrow{AC}\right|=\dfrac{1}{2}AC\)\(=a\sqrt{3}\).

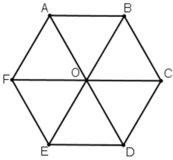
a: Vì ABCDEF nội tiếp (O) mà ABCDEF là đa giác đều nên AD,BE,CF là các đường kính của (O)
Xét tứ giác ABDE có
O là trung điểm của AD
O la trung điểm của BE
Do đó: ABDE là hình bình hành
Suy ra: \(\overrightarrow{AB}=\overrightarrow{ED}\)
b: Xét tứ giác AFDC có
O là trung điểm của AD
O là trung điểm của FC
Do đó; AFDC là hình bình hành
Suy ra: vecto AC=vecto FD

a: \(\overrightarrow{AB}=\overrightarrow{OC}=\overrightarrow{FO}=\overrightarrow{ED}\)
b: Vecto cùng phương với vecto AD là vecto BC, vecto OD, vecto FE
c: Vecto đối của vecto BC là vecto CB, vecto DO, vecto EF

a) Các vectơ khác vectơ O→ và cùng phương với vectơ OA→ là:
b) Các vectơ bằng vectơ AB→ là:

a) Ta có:
\(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}\)
\(=\overrightarrow{AB}+k\overrightarrow{BC}\)
\(=\overrightarrow{AB}+k\left(\overrightarrow{AC}-\overrightarrow{AB}\right)\)
\(=\left(1-k\right)\overrightarrow{AB}+k\overrightarrow{AC}\)
b) \(\overrightarrow{NP}=\overrightarrow{AP}-\overrightarrow{AN}\)
\(=\dfrac{2}{3}\overrightarrow{AC}-\dfrac{3}{4}\overrightarrow{AB}\)
Để \(AM\perp NP\)
\(\Rightarrow\overrightarrow{AM}.\overrightarrow{NP}=\overrightarrow{0}\)
\(\Rightarrow\left[\left(1-k\right)\overrightarrow{AB}+k\overrightarrow{AC}\right]\left(-\dfrac{3}{4}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}\right)=\overrightarrow{0}\)
\(\Leftrightarrow\dfrac{3\left(k-1\right)}{4}AB^2+\dfrac{2k}{3}AC^2+\dfrac{2\left(1-k\right)}{3}\overrightarrow{AB}.\overrightarrow{AC}-\dfrac{3k}{4}\overrightarrow{AB}.\overrightarrow{AC}=\overrightarrow{0}\)
\(\Leftrightarrow\dfrac{3\left(k-1\right)}{4}AB^2+\dfrac{2k}{3}AB^2+\dfrac{1-k}{3}AB^2-\dfrac{3k}{8}AB^2=0\)
\(\Leftrightarrow AB^2\left[\dfrac{3\left(k-1\right)}{4}+\dfrac{2k}{3}+\dfrac{1-k}{3}-\dfrac{3k}{8}\right]=0\)
\(\Leftrightarrow18\left(k-1\right)+16k+8\left(1-k\right)-9k=0\left(AB>0\right)\)
\(\Leftrightarrow17k=10\)
\(\Leftrightarrow k=\dfrac{10}{17}\)

A B C K G M D N
a, \(\Delta BKCcó\left\{{}\begin{matrix}BM=MC\\BG=GK\end{matrix}\right.\)
=> GM là đường trung bình của \(\Delta BKC\)
=> \(GM=\frac{1}{2}KC\)
\(\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AM}=6\overrightarrow{GM}=3\overrightarrow{KC}\)
b, \(\overrightarrow{AB}+3\overrightarrow{AC}=\overrightarrow{AD}+\overrightarrow{DB}+3\overrightarrow{AD}+3\overrightarrow{DC}\)
\(=4\overrightarrow{AD}+\left(-3\overrightarrow{DC}\right)+3\overrightarrow{DC}\)
\(=4\overrightarrow{AD}\)
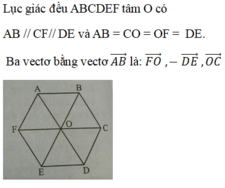
Gọi O là tâm của lục giác đều thì dễ thấy ABOF là hình bình hành
\(\Rightarrow\overrightarrow{AB}+\overrightarrow{AF}=\overrightarrow{AO}\)
Mà \(\overrightarrow{AO}=\dfrac{1}{2}\overrightarrow{AD}\) \(\Rightarrow\overrightarrow{AB}+\overrightarrow{AF}=\dfrac{1}{2}\overrightarrow{AD}\)
\(\Rightarrow k=\dfrac{1}{2}\)
-> Chọn B